深度优先搜索DFS理解与应用
需积分: 10 140 浏览量
更新于2024-09-11
收藏 326KB PDF 举报
"DFS个人心得分享,探讨深度优先搜索与广度优先搜索的差异和适用场景"
深度优先搜索(DFS)是一种在图或树结构中遍历所有节点的算法,其核心思想是从一个起始节点开始,尽可能深入地探索路径,直到无法继续前进时才回溯到上一个节点,尝试其他分支。DFS常用于解决路径查找、是否存在环路、连通性等问题。
1. **DFS的基本流程**
- 从给定的起始节点开始。
- 访问当前节点并标记为已访问,防止重复访问。
- 探索当前节点的所有未访问邻接节点,选择一个继续深入。
- 如果达到目标节点或无法继续探索,回溯至上一节点,重复步骤3。
- 这个过程持续到所有可达节点都被访问。
2. **DFS与BFS的对比**
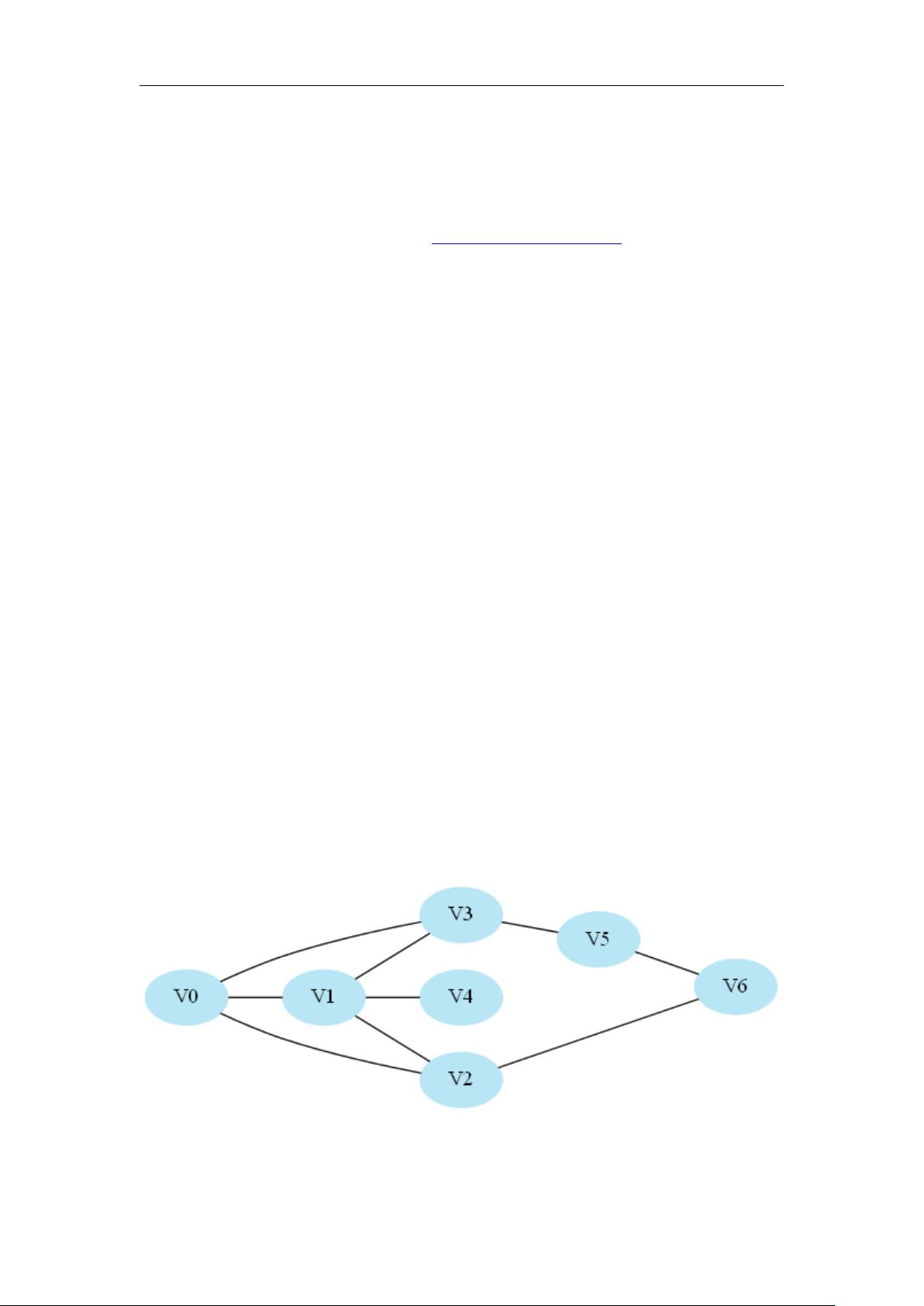
- **DFS** 演示过程:在给定的例子中,从V0出发,先尝试V1->V4,无法到达V6,然后回溯到V1,再尝试V2,最终找到V6。DFS往往能更快找到一条路径,但不保证是最短路径。
- **BFS**(广度优先搜索):从V0开始,按层次顺序探索,会先访问所有同一层次的节点,再进入下一层。BFS适合找最短路径,但需要更多内存,尤其在节点子节点数大且层次深时。
3. **DFS的优缺点**
- 优点:DFS通常内存消耗较小,因为它仅需存储一条路径,适用于解决连通性问题和查找路径。
- 缺点:可能无法找到最优解,比如最短路径问题。并且,如果图中有环,可能会陷入无限循环。
4. **应用场景**
- **拓扑排序**:在无环有向图中,DFS可以用于拓扑排序,确定节点的相对顺序。
- **迷宫问题**:DFS可以用来寻找迷宫中的出路。
- **二叉树操作**:在二叉树中,DFS可以用于遍历所有节点,例如前序、中序和后序遍历。
- **判断图的连通性**:通过DFS遍历所有节点,如果每个节点都能访问到,则图是连通的。
5. **DFS的实现方式**
- 递归实现:直接通过函数调用来实现深度优先遍历。
- 栈实现:利用栈的后进先出特性模拟递归过程。
6. **优化策略**
- 使用**剪枝**技术可以在搜索过程中提前结束不必要的分支,减少计算量。
- 使用**记忆化**技术避免重复计算,提高效率。
7. **注意事项**
- 在实现DFS时,需要注意避免回环,通常通过标记已访问节点来处理。
- 对于复杂图结构,可能需要结合其他数据结构如并查集、堆等来优化DFS。
总结,DFS和BFS各有其特点和适用范围,选择哪种方法取决于具体问题的需求。理解它们的工作原理和优缺点是解决问题的关键。在实际应用中,根据问题的特性和资源限制灵活选择或结合使用这两种搜索策略。
2021-11-23 上传
2021-10-04 上传
2022-01-22 上传
WingFlyHigh
- 粉丝: 0
- 资源: 1
最新资源
- NotesAppJavascriptPractice:针对教程
- modelando-dominios-ricos-java:该项目旨在应用在AndréBaltieri的“建模富域”课程中介绍的概念。 关联
- MySQLtoHDF5:将 MySQL 数据库转换为 HDF5 文件
- mamamoneybookmarks:包含用于妈妈钱的书签列表
- AT89S51+MAX232+CD4053B+9014组成的原理图
- 1-求职简历-word-文件-简历模版免费分享-应届生-高颜值简历模版-个人简历模版-简约大气-大学生在校生-求职-实习
- qownnotes-overlay:QOwnNotes覆盖
- jsx-slack:从JSX为Slack Block Kit表面构建JSON对象
- JS_forelasning_1
- Ideal-Zen-Refonte-2021:理想的Zen Refonte 2021
- tabcmd_linux:在 Linux 中实现 Tableau 的 tabcmd 命令行实用程序
- Bdae
- Project-61160014-61160222
- Mysql学习并训练.zip
- 链表数据结构
- karashirl.github.io:项目组合