N=4 SYM中雷格振幅的全环猜想：新粘合操作与Wilson线积分

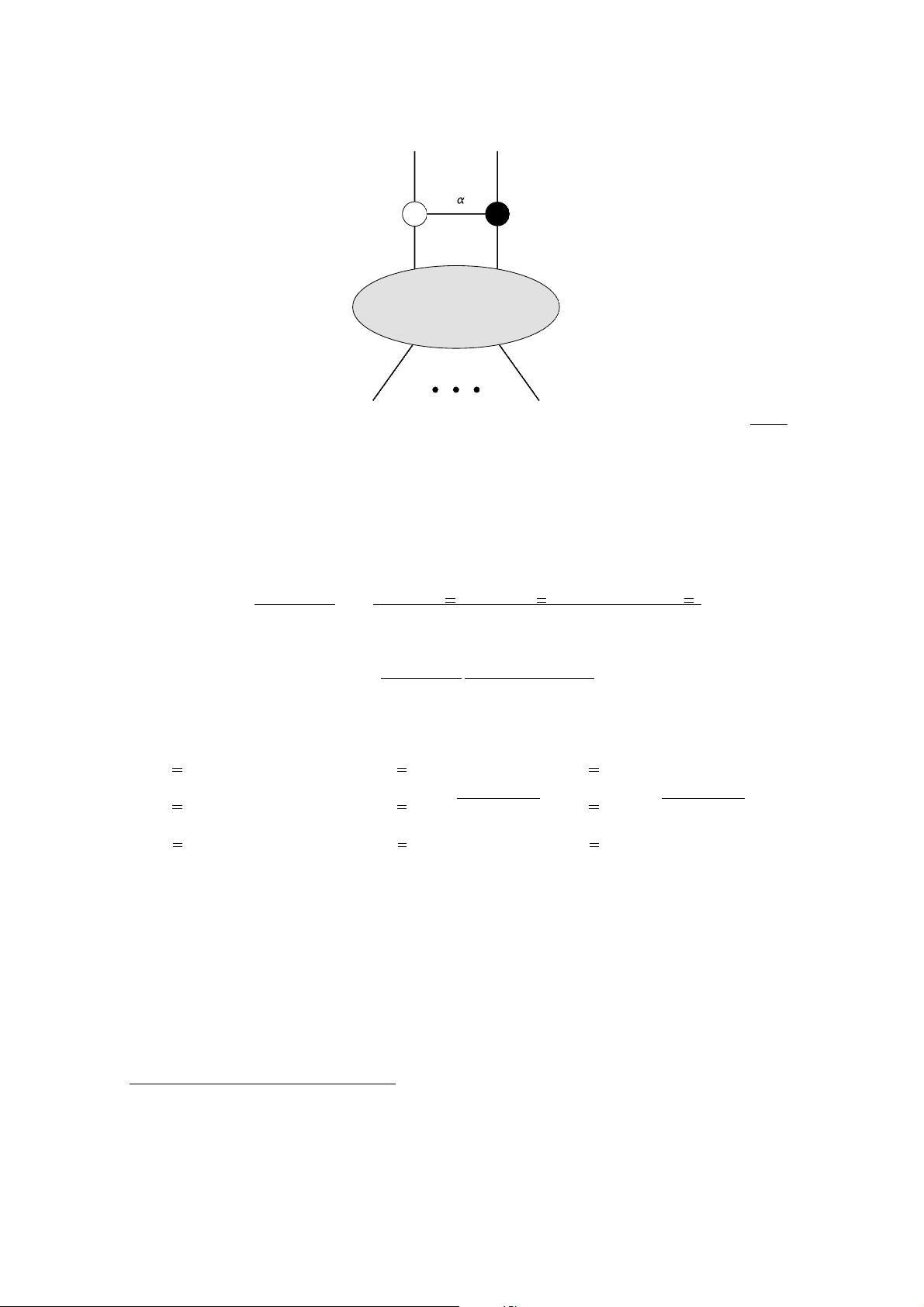
本文探讨了N = 4超 Yang-Mills (SYM)理论中的雷格振幅积分问题，这是一种在量子色动力学（QCD）的广义化形式中，特别是在研究多粒子散射过程中的非perturbative行为时至关重要的概念。雷格振幅，也被称为Reggeon amplitudes，是描述散射过程中高能粒子对之间的交换对象的特性。在N = 4 SYM中，这些振幅的全环猜想是指一个关于所有阶次的积分被积形式的预测，它对于理解粒子间相互作用的非平凡结构至关重要。 作者们提出了一个新的粘合操作，这是一个在动量扭曲空间中的构造，这是一种在数学上抽象的物理空间，将粒子的相位空间与超对称理论中的几何概念联系起来。通过这种粘合过程，他们能够从基本的壳层（Reggeon tree-level amplitudes）表达式出发，推导出雷根树级幅度和循环积分的递归公式。这种方法类似于BCFW（Britto-Cachazo-Feng-Witten）递归关系，它在计算高能物理中的相关量时具有重要意义。 文章还涉及到循环级别的雷根循环积分的预测，这些积分是通过局部积分技术编写的，它们对于验证粘贴操作在循环精度下的正确性至关重要。循环积分的精确计算在理解高能物理的渐近行为和确定粒子散射的幂律行为方面发挥关键作用。 为了检验这一粘合操作的效力，作者们进一步导出了N = 4 SYM中的低阶贝克斯特罗姆-弗朗基尔-库尔特（BFKL）内核表达式，这是在量子场论中描述强相互作用中粒子对散射的一种重要工具。BFKL方程是描述高能下粒子对散射过程中因子化性质的关键部分，特别是在洛伦兹不变的正规子群对称性下。 这篇文章的主要贡献在于提出了一种全新的方法来处理N = 4 SYM中的雷格振幅积分，并且提供了一个完整的理论框架，包括新的粘合操作、循环积分的预测以及对LO BFKL内核的计算。这些成果不仅深化了我们对量子色动力学的理论理解，也为未来的计算物理实验提供了强有力的理论支持。