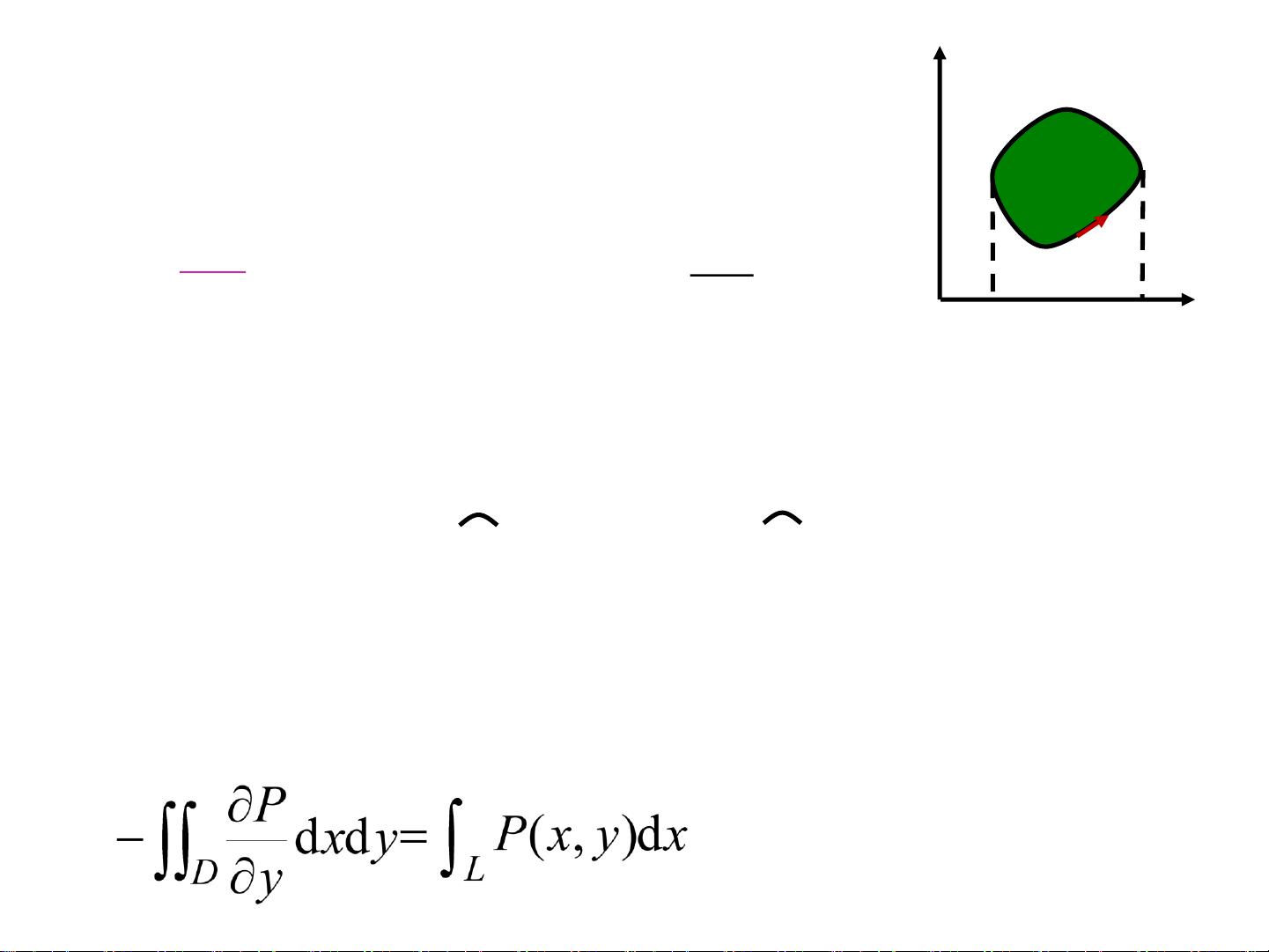格林公式的简单应用与区域连通性分类
需积分: 0 65 浏览量
更新于2024-01-31
收藏 1.14MB PDF 举报
"3-6.3-1格林公式1;第三节 格林公式(一)二、格林公式一、区域连通性的分类五、原函数三、格林公式的简单应用四、平面上曲线积分与路径无关条件一、区域连通性的分类1. 设D为平面区域,;第三节 格林公式(一)二、格林公式一、区域连通性的分类五、原函数三、格林公式的简单应用四、平面上曲线积分与路径无关条件一、区域连通性的分类1. 设D为平面区域, 如果D内任一闭曲线所围成的部分都属于D, 则称D为平面单连通区域, 否则称为复连通区域(多连通区域、非单连通区域).复连通区域单连通区域DD有洞的区域.无洞的区域2. 简单曲线:没有交点的曲线.简单闭曲线:只有起点和终点才重合的曲线.连成与由21LLL组成与由21LLL2LD1L2L1LD3. 区域 D 边界L 的正向: 沿L的这个方向行走时D总在行走者的左边.注:几何上看,平面单连通区域边界线的正向是逆时针方向;复连通区域边界线的正向是外边界线是逆时针方向,内边界线是顺时针方向.定理1. 设区域 D 是由光滑或分段光滑的简单闭则有dd =d dLDQPP xQ yx yxy( 格林公式 )一阶连续偏导数,二、 格林公式曲线 L 所围成, 函数在 D 上具有其中, L 是 D 的正向边界曲线.证明: 1) 若D 既是 X - 型 又是 Y -型的单连通区域, 则yxxQDdd ;"
格林公式是数学中的一个重要定理,用于计算平面上曲线积分与路径无关的条件。该定理包含了区域连通性的分类,原函数的概念,以及格林公式的简单应用。
区域连通性的分类是指根据区域的特性将其分为平面单连通区域和复连通区域。平面单连通区域指闭曲线所围成的部分都属于该区域,没有洞的区域。而复连通区域则是指存在闭曲线所围成的部分不属于该区域,有洞的区域。简单曲线是指没有交点的曲线,而简单闭曲线是指只有起点和终点重合的曲线。
区域D的边界L的正向是指沿L的方向行走时,区域D总在行走者的左边。对于平面单连通区域,边界线的正向是逆时针方向;对于复连通区域,外边界线的正向是逆时针方向,而内边界线的正向是顺时针方向。
格林公式表述了在区域D中存在连续一阶偏导数的函数f(x, y),其对于曲线L所围成的面积的曲线积分等于对D内部区域的偏导数的面积积分。其中L是D的正向边界曲线,而Q是f的某个原函数。
证明中提到了若区域D既是X型又是Y型的单连通区域,那么通过格林公式计算曲线积分时可简化为对D区域进行积分的形式。
总结而言,格林公式是一个关于区域连通性、曲线积分与路径无关条件的定理。它在数学和物理等领域有着广泛的应用,能够简化复杂的积分计算,并提供了一种判断区域连通性的方法。该定理深入浅出地描述了曲线积分与区域内函数的关系,为数学领域的研究和应用提供了重要的工具。
2022-08-04 上传
2022-08-03 上传
2022-08-03 上传
2024-11-04 上传
2024-11-04 上传
2024-11-04 上传
2024-11-04 上传
嘻嘻哒的小兔子
- 粉丝: 34
- 资源: 321
最新资源
- Aspose资源包:转PDF无水印学习工具
- Go语言控制台输入输出操作教程
- 红外遥控报警器原理及应用详解下载
- 控制卷筒纸侧面位置的先进装置技术解析
- 易语言加解密例程源码详解与实践
- SpringMVC客户管理系统:Hibernate与Bootstrap集成实践
- 深入理解JavaScript Set与WeakSet的使用
- 深入解析接收存储及发送装置的广播技术方法
- zyString模块1.0源码公开-易语言编程利器
- Android记分板UI设计:SimpleScoreboard的简洁与高效
- 量子网格列设置存储组件:开源解决方案
- 全面技术源码合集:CcVita Php Check v1.1
- 中军创易语言抢购软件:付款功能解析
- Python手动实现图像滤波教程
- MATLAB源代码实现基于DFT的量子传输分析
- 开源程序Hukoch.exe:简化食谱管理与导入功能