GARCH模型在金融数据中的应用：沪深股市波动研究

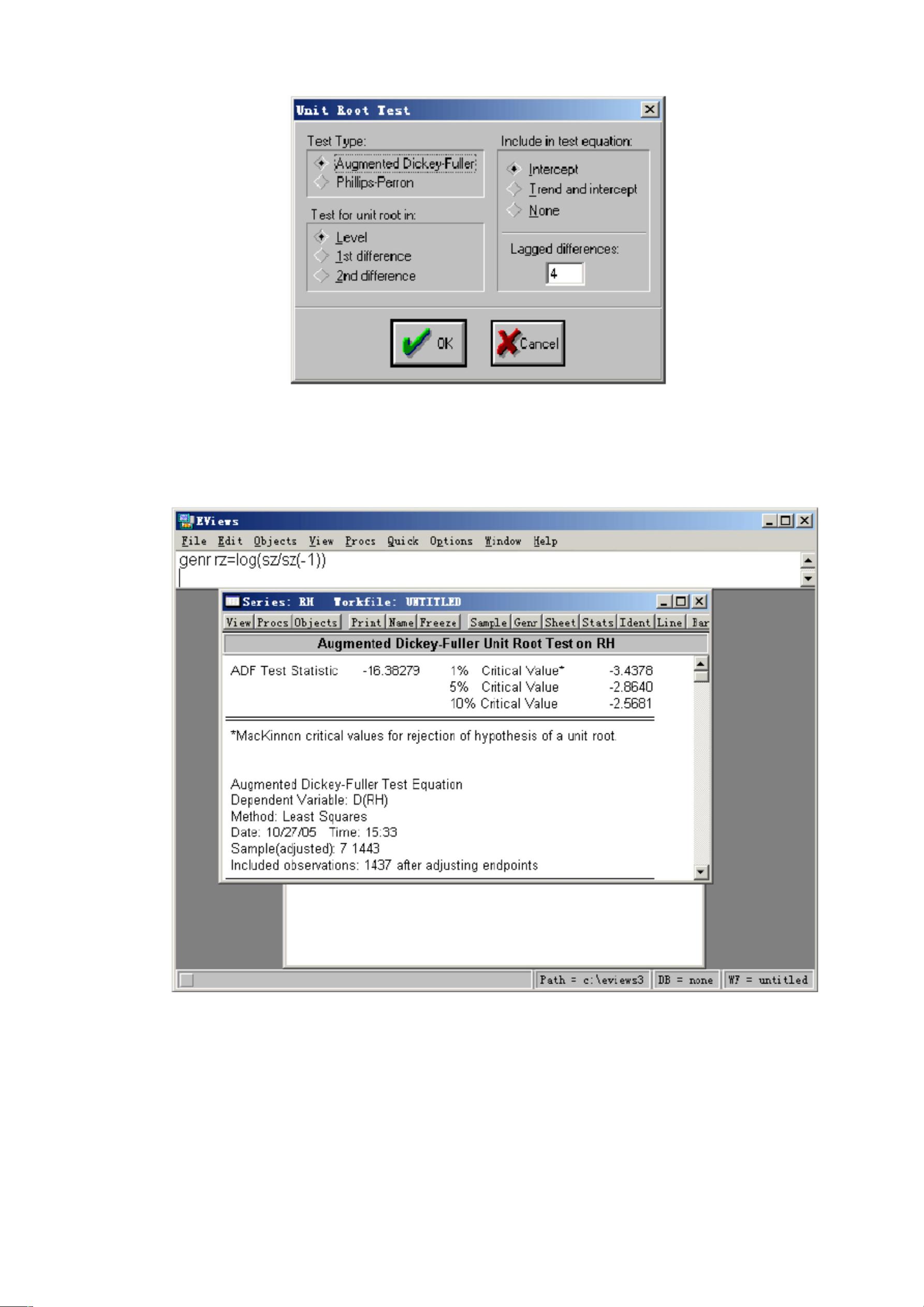
"实验七GARCH模型在金融数据中的应用" GARCH（Generalized AutoRegressive Conditional Heteroskedasticity）模型是一种广泛应用于金融数据分析的统计模型，它用于描述时间序列数据的波动性，特别是在金融领域，如股票市场、汇率、利率等的波动性分析。GARCH模型能够捕捉到数据的动态变化特征，即条件方差不是常数，而是与过去的观测值和方差有关。 实验七的主要目的是让学生理解和掌握自回归异方差（ARCH）模型及其扩展形式GARCH模型的基本概念、应用场景和不同变体。ARCH模型是GARCH模型的基础，它假设当前的残差平方与过去一段时间的残差平方有线性关系，即条件方差依赖于过去一段时间的误差项的平方。在公式中，\( h_t \) 表示第t时刻的条件方差，\( a_0, a_1, ..., a_p \) 是模型参数，\( \epsilon_{t-1}, ..., \epsilon_{t-p} \) 是过去的残差平方。 GARCH模型进一步扩展了这一思想，不仅考虑过去的残差平方，还考虑了过去条件方差的影响，这在GARCH(p, q)模型中体现，其中p表示自回归项的阶数，q表示移动平均项的阶数。GARCH-M模型（GARCH in mean）将条件方差引入均值方程，EGARCH模型（Exponential GARCH）采用了指数形式来处理负冲击的影响，而TARCH（GJR-GARCH）模型则考虑了负面和正面冲击的不同影响，尤其在金融市场的回弹效应（leverage effect）。 实验内容要求学生基于上证指数和深证成指的数据，进行以下研究： 1. 波动性研究：通过计算收益率的统计特性，如均值、标准差、偏度和峰度，来探究股市的波动性。 2. 非对称性研究：GJR-GARCH模型可以检测到正负冲击对波动的不同响应，这有助于理解市场的不对称性。 3. 溢出效应研究：分析两个市场之间是否存在波动传染，即一个市场的异常波动是否会影响另一个市场的波动。 实验要求学生深入理解理论，对实验步骤进行实践，并能熟练使用Eviews软件进行数据处理和模型估计。通过这个实验，学生将能够应用GARCH模型进行实证研究，理解金融数据的波动性动态，并可能发现金融市场中的有趣现象和规律。