Mathematica实现线性代数：矩阵操作与运算解析

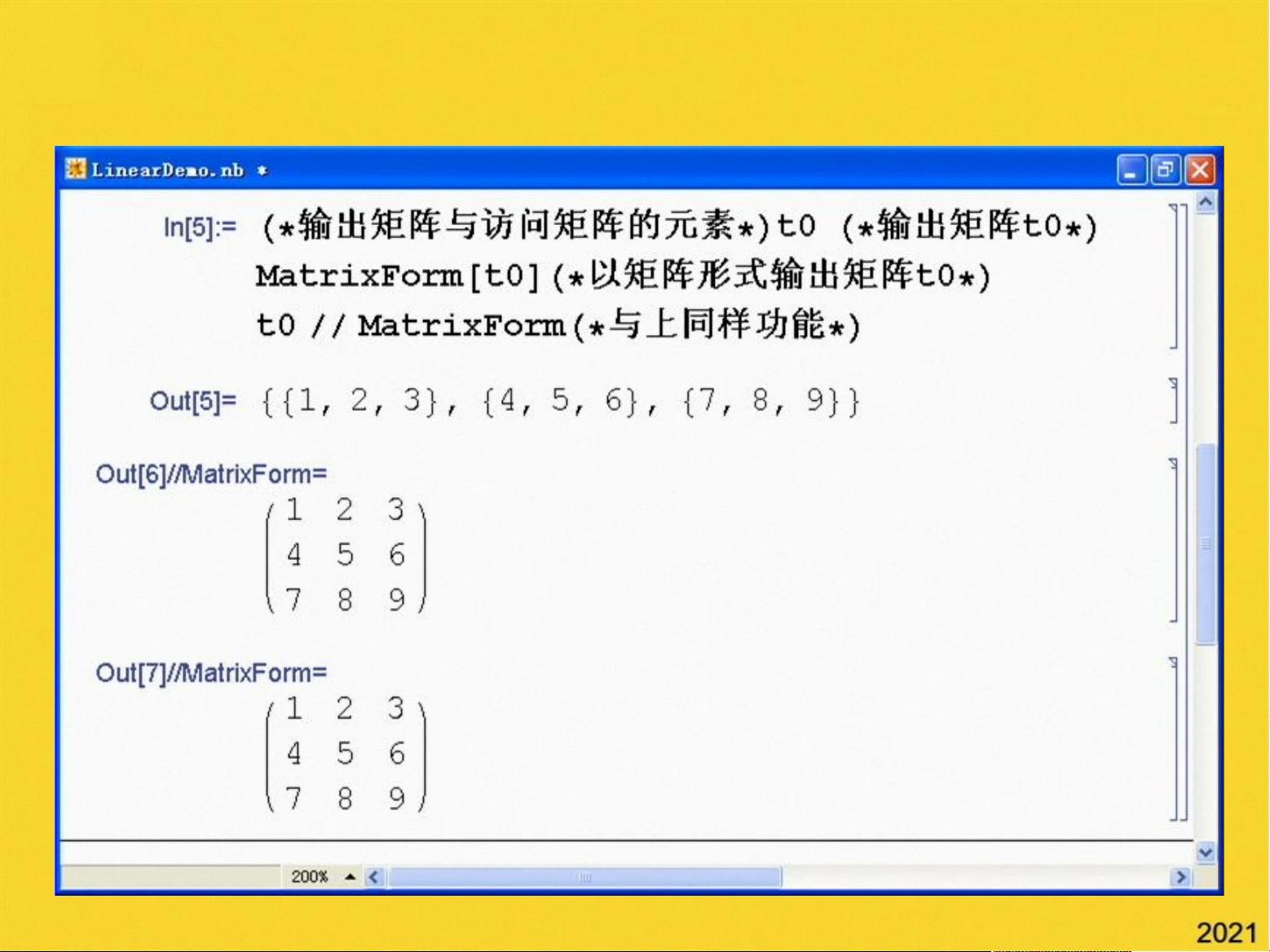
"该资源为线性代数基本问题的软件实现教程，共计32页PPT，主要讲解如何在Mathematica中进行矩阵的构造、运算和相关操作。" 线性代数是数学的一个重要分支，它在计算机科学、物理学、工程学等多个领域都有着广泛的应用。本教程聚焦于线性代数中的基本问题，特别是如何利用软件工具Mathematica进行计算和分析。Mathematica是一款强大的数学软件，能够方便地进行数值计算、符号计算以及图形绘制。 1. **矩阵构造与输入** 在Mathematica中，矩阵可以被视为数表来创建。例如，键入`tt={a,b,c}`会创建一个3维向量`{a,b,c}`，而`t0={{1,2,3},{4,5,6}}`则会构建一个2x3的矩阵`t0`。此外，可以通过工具栏或菜单来输入矩阵，对矩阵的行和列进行增加或删除。 2. **矩阵运算** 矩阵运算包括提取特定元素（如`t0[[1,2]]`代表第一行第二列的元素）、矩阵的加减乘法、数乘、转置以及行列式等。Mathematica提供了丰富的函数来支持这些运算，如`Transpose[A]`用于求矩阵A的转置，`Length[list]`和`Dimensions[list]`分别用于获取列表的长度和维度，`Eigenvalues[N[A]]`用于计算矩阵A的特征值。 3. **系统函数生成矩阵** Mathematica内置了许多生成向量和矩阵的命令，如`Table`函数可以生成特定序列的向量，例如`Table[f,{i,m},{j,n}]`将生成一个由f(i,j)定义的m×n矩阵。此外，还有如`GramSchmidt`函数，用于执行Gram-Schmidt正交化过程，对一组向量进行正交化处理。 4. **矩阵的基本运算** 常规的矩阵运算在Mathematica中可以便捷地完成。例如，加法和减法只需将两个矩阵相加或相减，乘法则需注意矩阵的乘法规则（即行乘列）。矩阵的逆可以通过调用相应的函数求得，这对于解线性方程组或进行其他线性变换非常关键。 5. **其他功能** 除了基本的矩阵运算外，Mathematica还支持更复杂的线性代数操作，如特征值分解、奇异值分解、解线性方程组等。这些高级功能使得Mathematica成为研究和教学线性代数的强大工具。 本教程通过具体的示例和操作步骤，旨在帮助学习者掌握如何在Mathematica环境中高效地处理线性代数问题，从而更好地理解和应用线性代数理论。通过学习，用户将能够利用Mathematica解决实际问题，提升计算能力，并为后续的科学研究或工程应用打下坚实的基础。