图的术语与定义解析：有向图与无向图

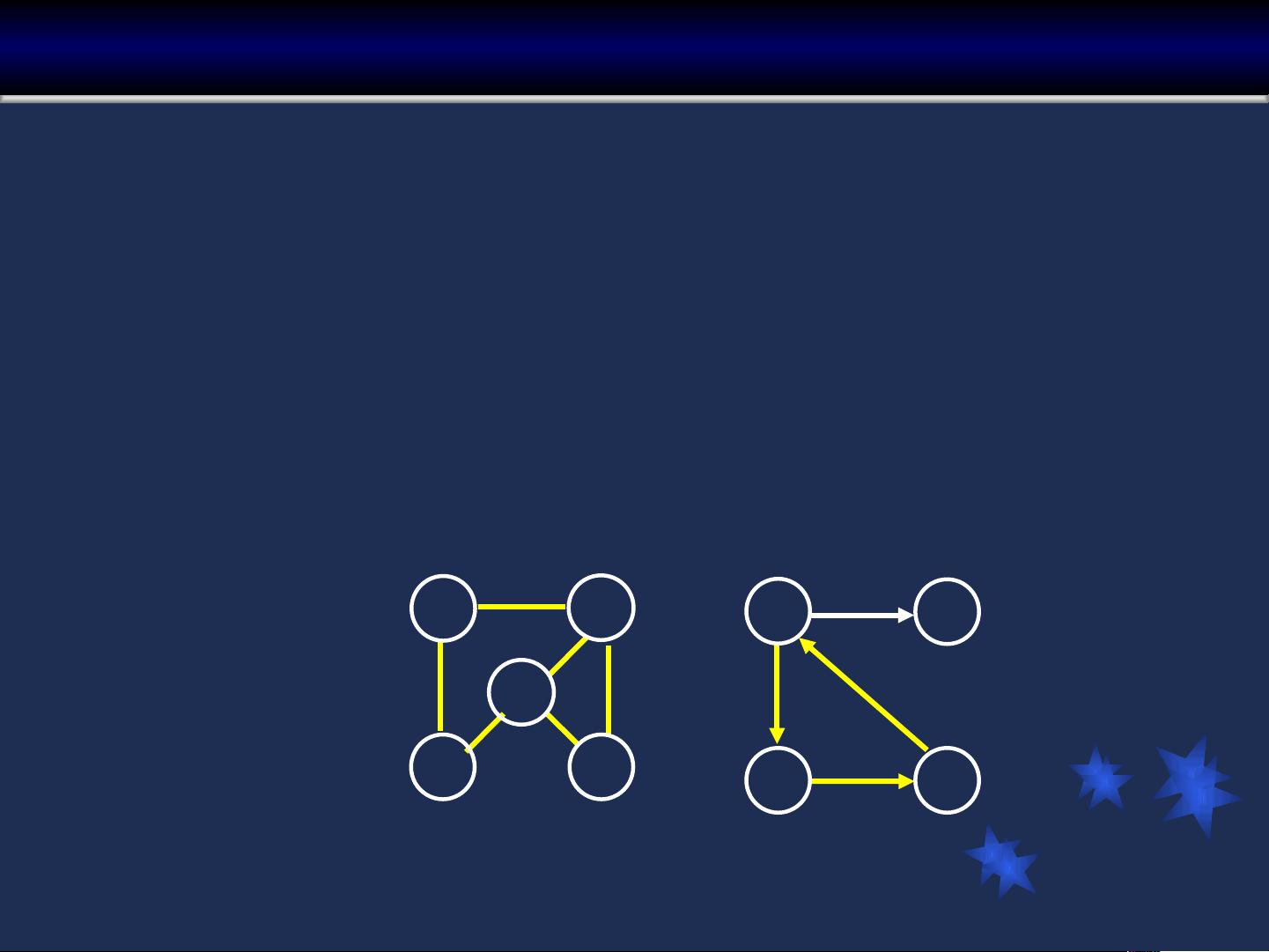
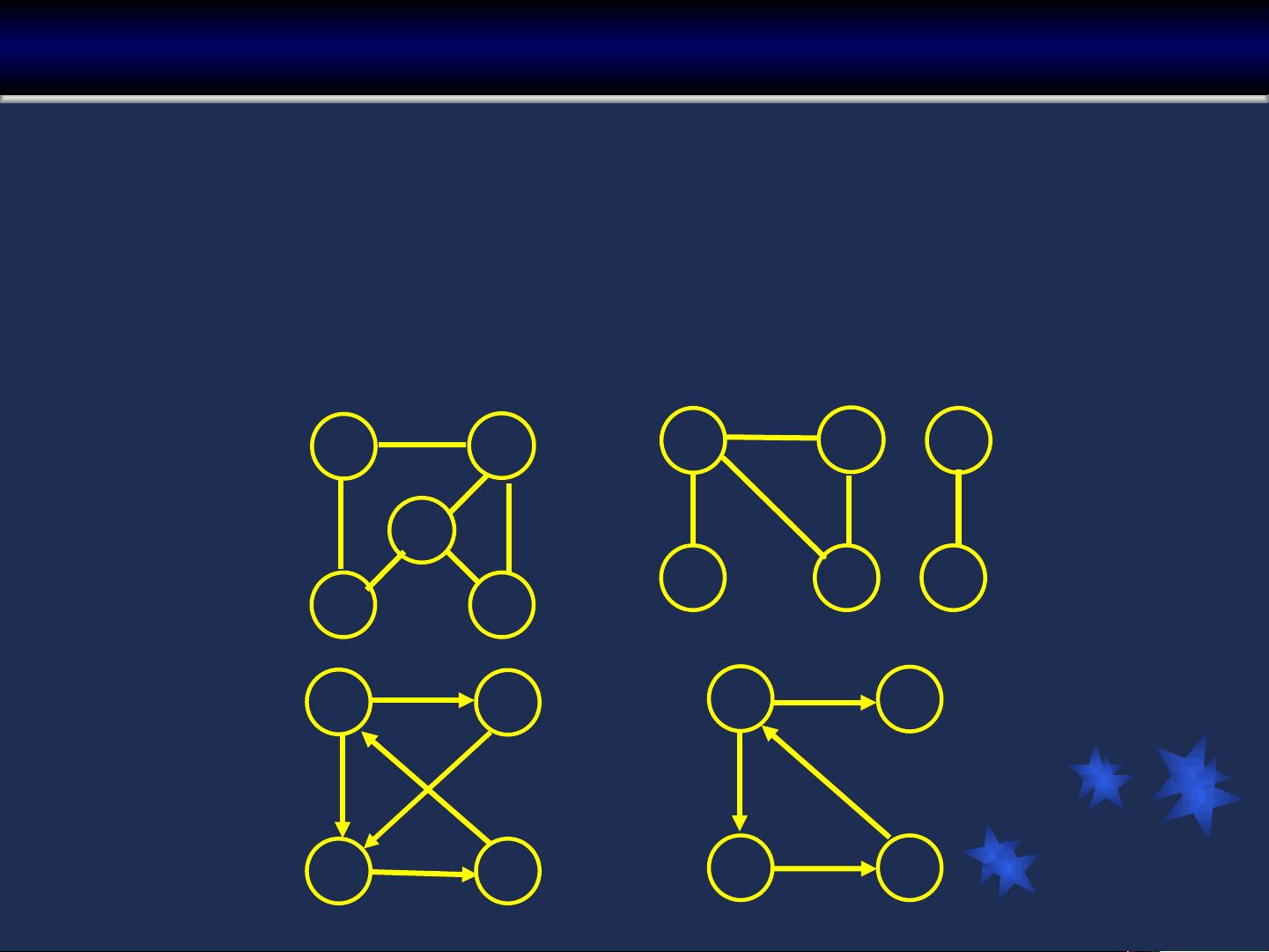
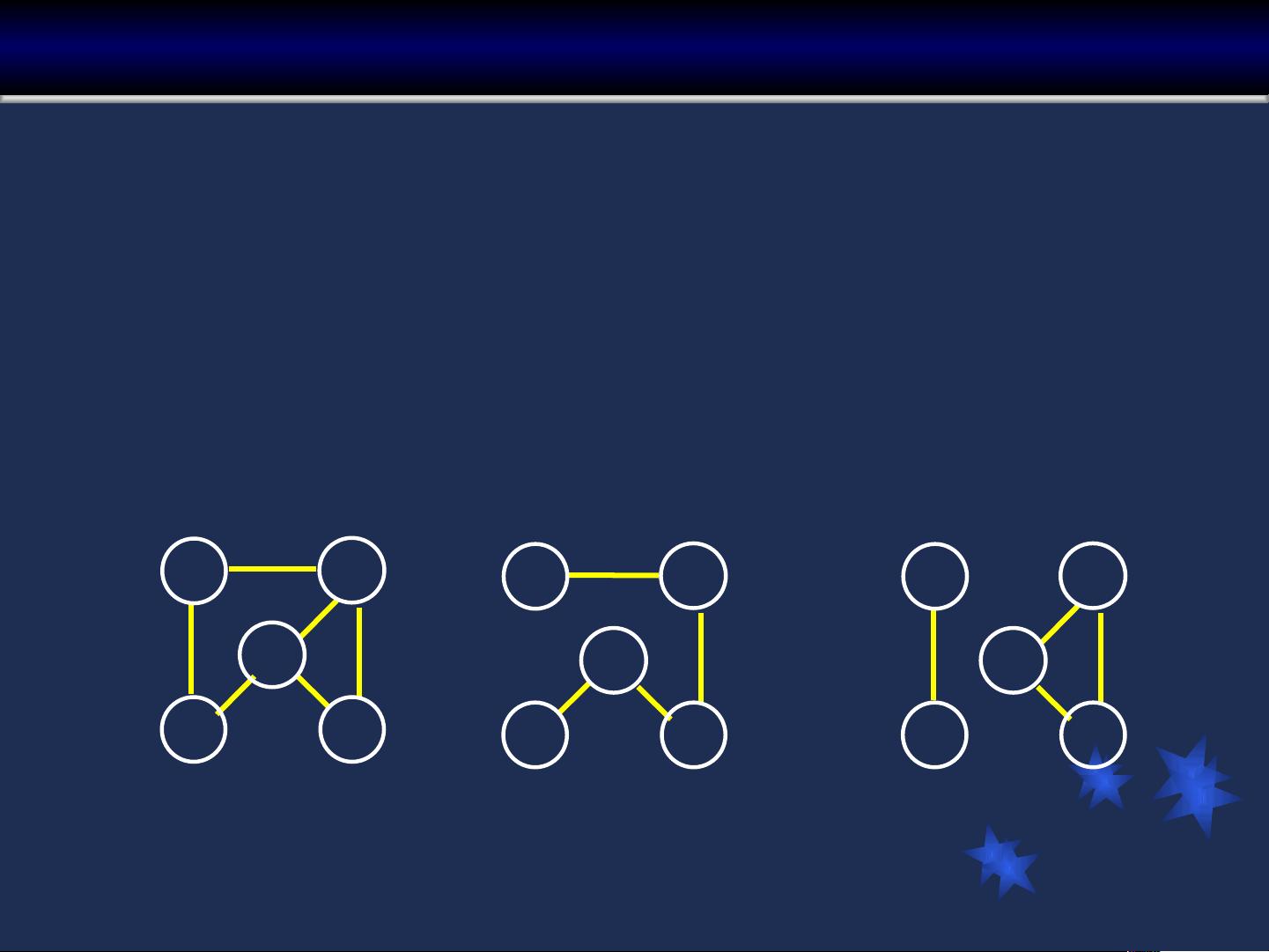
"数据结构课件：第7章 图.ppt" 在计算机科学中，数据结构是组织和存储数据的方式，而图作为一种重要的数据结构，广泛应用于解决各种问题，如网络设计、路径规划、社交网络分析等。本课件详细介绍了图的概念、分类及其基本术语。 首先，图（Graph）由两个集合构成：顶点集V(G)和边集E(G)，通常表示为G=(V,E)。顶点集V(G)是非空的有限集合，代表图中的各个元素或节点；边集E(G)则包含顶点间的连接关系，可以是无序对（无向图）或有序对（有向图）。 有向图（Directed Graph）是边具有方向性的图，每条边（又称弧）由一个顶点指向另一个顶点，用有序对<v,w>表示，其中v是弧尾，w是弧头。例如，图G1中包含顶点A、B、C、D、E，以及若干有向边如<A,B>、<A,E>等。 无向图（Undirected Graph）的边没有方向性，用无序对(v,w)表示，且(v,w)等于(w,v)。图G2包含顶点v0、v1、v2、v3、v4，以及无向边如(v0,v1)、(v0,v3)等。在无向图中，如果两个顶点之间有一条边，我们说它们是邻接点，边称为关联边。每个顶点的度是与其关联边的数量。 图的应用非常广泛，如交通图中，顶点代表地点，边代表连接地点的公路或铁路；电路图中，顶点代表元件，边代表元件间的线路；通讯线路图中，顶点代表地点，边代表地点间的通信线路；在流程图中，顶点表示工序，边则表示工序之间的顺序关系。 对于有向图，每个顶点有两个度数：入度（In-degree）和出度（Out-degree），分别表示以该顶点为终点和起点的边数。顶点的度是入度和出度之和。而在无向图中，顶点的度就是其关联边的数量。图论的一个重要定理是，对于任何无向图或有向图G，所有顶点的度数之和等于边数的两倍，这是因为每条边贡献了两个顶点的度数。 了解这些基础概念后，可以进一步探讨图的遍历算法（如深度优先搜索和广度优先搜索）、图的最小生成树（如Prim算法和Kruskal算法）、最短路径问题（如Dijkstra算法和Floyd-Warshall算法）以及图的矩阵表示（邻接矩阵和邻接表）等高级主题。掌握图的数据结构及其操作是计算机科学中至关重要的技能，对于理解和解决复杂问题具有极大的帮助。