FFT算法详解与应用实践

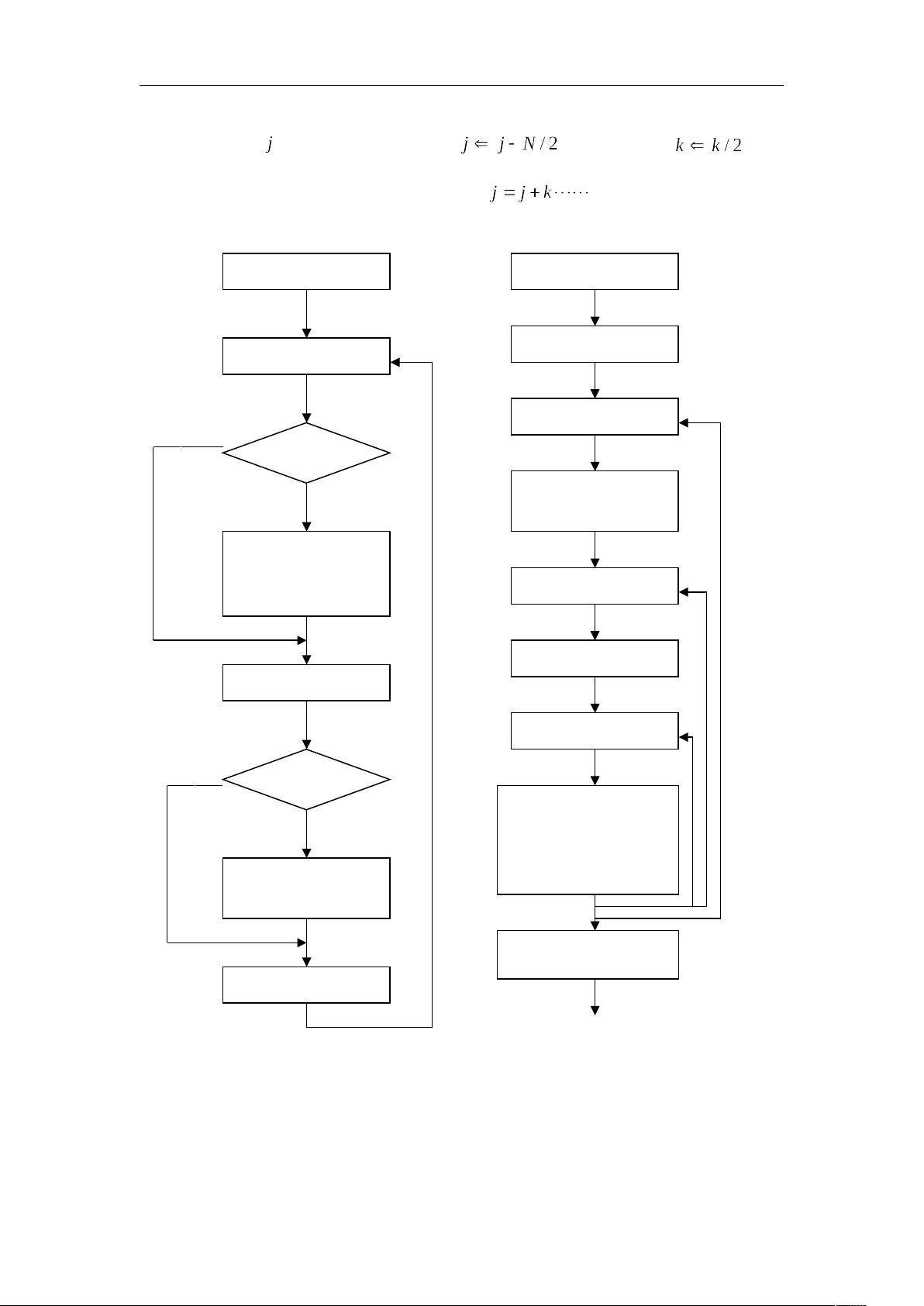
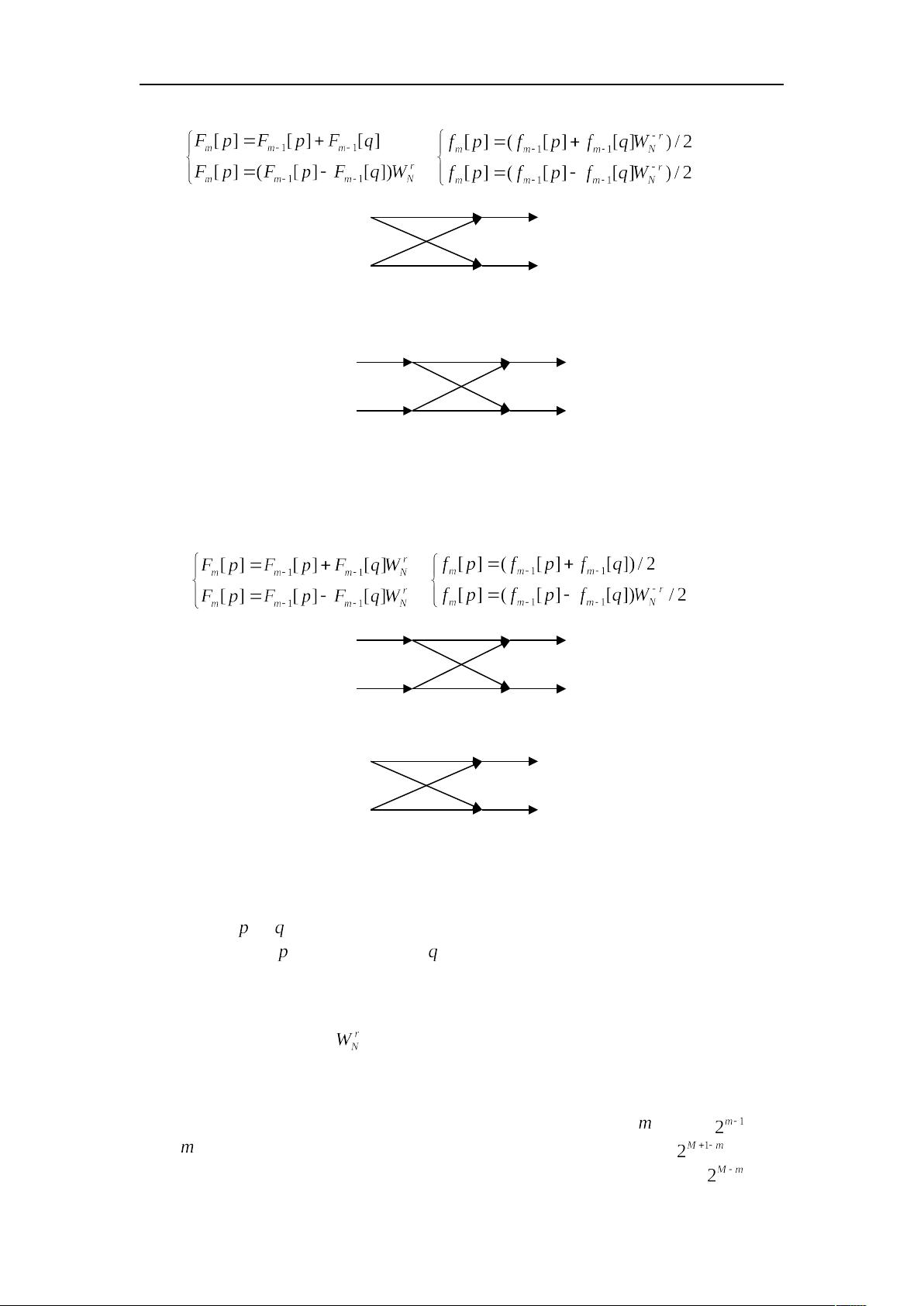
"快速傅里叶变换(FFT)是一种高效计算离散傅里叶变换(DFT)的算法，广泛应用于数字信号处理、图像处理、通信工程等领域。本文详细介绍了FFT算法的原理和实现，包括一维和二维的情况，并通过Matlab编程给出了具体应用实例。" 快速傅里叶变换FFT算法是基于分治策略的优化算法，它显著减少了计算离散傅里叶变换所需的时间复杂度，从DFT的原始O(N^2)降低到O(N log N)，其中N是数据序列的长度。FFT算法主要分为基2 FFT和非基2 FFT。 对于基2 FFT，又分为频域抽取和时域抽取两种方法。频域抽取FFT算法是通过对DFT的结果进行对半拆分，然后递归计算，而时域抽取FFT则是通过对输入序列进行对半拆分，再进行递归计算。这两种方法在计算过程中都涉及到蝶形运算，这是FFT的核心操作。 1. 频域抽取的基2 FFT算法： - 正变换：首先将序列分成偶数项和奇数项，分别进行DFT，然后将结果相加和相减，形成新的序列。 - 逆变换：与正变换类似，但相加和相减的操作顺序相反，还需要除以N来得到正确的逆变换。 2. 时域抽取的基2 FFT算法： - 正变换：对序列进行位移，然后将序列分成偶数项和奇数项，分别进行DFT，最后进行复数乘以W_n，其中W_n是复数单位根。 - 逆变换：与正变换类似，但复数乘以W_n的操作需要使用W_n的共轭。 对于非基2 FFT，主要有Cooley-Tukey算法和素因子算法(PFA)。Cooley-Tukey算法是将非基2的DFT分解成更小的基2 DFT，而PFA是将DFT分解为更简单的因子，如直接计算较小规模的DFT。 1. Cooley-Tukey FFT算法：通过分解DFT为若干个基2 DFT，然后递归计算，可以适应任意大小的N。 2. 素因子算法(PFA)：当N是合数时，PFA将N分解为其素因子，然后分别计算这些素因子对应的DFT，最后组合起来得到整个DFT。 FFT算法在数字信号处理中有多种应用，例如： - 计算连续时间信号的傅里叶变换，用于频谱分析。 - 计算离散信号的线性卷积，如在滤波器设计中。 - 离散信号压缩，如在音频或图像编码中。 - 滤波，通过设计合适的滤波器函数，对信号进行频率选择性增强或抑制。 本文通过流程图、表格和Matlab编程实例，深入浅出地展示了FFT算法的细节，方便读者理解和应用。二维FFT算法则是在一维FFT基础上扩展，用于处理矩阵或图像数据，同样具有高效性。 总结来说，FFT算法是计算大规模离散傅里叶变换的关键工具，它的高效性和广泛应用使得它成为信号处理领域不可或缺的一部分。本文不仅提供了理论知识，还提供了实用的编程示例，有助于读者掌握FFT算法并应用于实际问题。