正态分布详解：概念、特征与应用

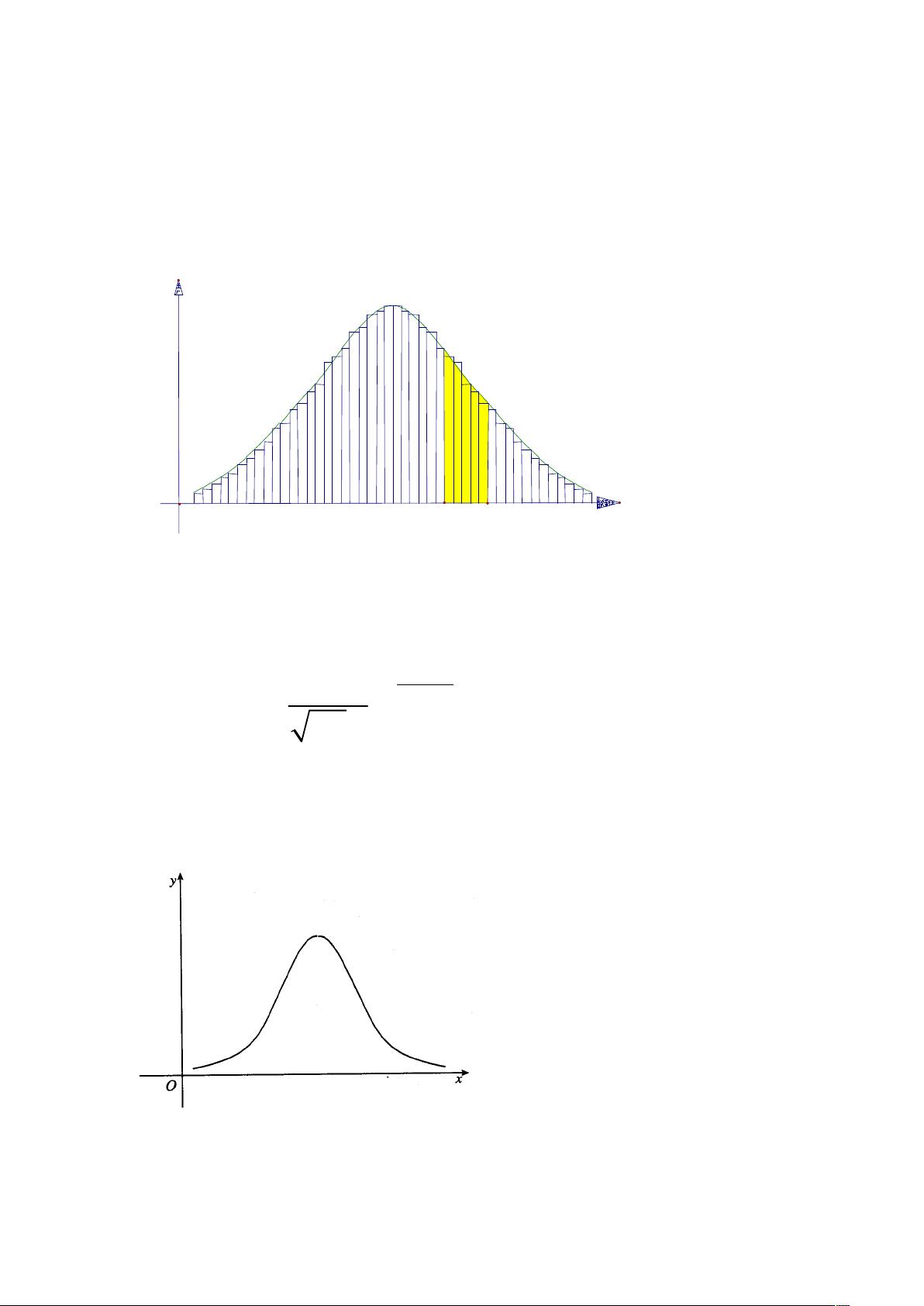
"正态分布是一种在统计学和概率论中常见的连续概率分布，具有对称的钟形曲线，通常用于描述许多随机变量的分布情况，比如自然现象、生产过程中的误差、人体测量数据等。正态分布有两个关键参数，即平均数μ和标准差σ，它们决定了分布的中心位置和形状。平均数μ代表了数据集的中心趋势，而标准差σ则描述了数据点相对于平均数的离散程度。 正态分布的密度函数可以表示为f(x)=1/(σ√(2π)) * e^(-((x-μ)^2)/(2σ^2))，其中e是自然对数的底数。这个函数形成的曲线称为正态曲线，当x=μ时，曲线达到最高点，而曲线的宽度由标准差σ决定，σ越大，曲线越宽，表示数据的变异程度更大。 在正态分布中，关于平均数μ的对称性意味着数据的50%位于μ之上，50%位于μ之下。此外，特定的百分位数可以通过查正态分布表或者使用Z分数（标准化得分）来确定。例如，标准正态分布（μ=0, σ=1）中，Z=1对应于分布的上方16%的数据，Z=-1对应于下方16%，而Z=2则对应于上方2.33%的数据。 在实际应用中，如果一个随机变量X服从正态分布，我们通常记为X～N(μ, σ^2)，这里的N表示正态分布，括号内的参数分别表示平均数和方差（标准差的平方）。正态分布的重要性在于其广泛的应用，许多自然和人为过程产生的数据往往近似于正态分布，这使得我们可以利用正态分布的特性进行数据分析，如预测、假设检验和置信区间的计算。 在历史上，正态分布的理论由多位数学家发展，包括棣莫弗和高斯。高斯在研究测量误差时对正态分布进行了深入研究，因此正态分布有时也被称作高斯分布。正态分布不仅在概率统计中占据核心地位，也是许多其他统计方法（如t检验、F检验和卡方检验）的基础。 了解并掌握正态分布的概念和性质，对于理解和应用统计学至关重要。在实际问题中，我们常常需要通过样本数据估计总体的平均数和标准差，进而判断数据是否符合正态分布，这对于理解数据的内在规律和做出科学决策有着重要的指导意义。"