图论应用:最小生成树模型及其在电话线网络中的应用
版权申诉
137 浏览量
更新于2024-06-29
收藏 997KB PDF 举报
"最小生成树模型与实验.pdf"
在图论和数据挖掘领域,最小生成树模型是一个重要的概念,尤其在计算机科学(cs)中有着广泛的应用。最小生成树(Minimum Spanning Tree, MST)是图论的一个核心问题,主要解决在加权无向图中找到连接所有顶点的边的集合,使得这些边的总权重尽可能小。这个模型通常用于网络设计,例如电信网络规划、运输路线优化和资源分配等问题。
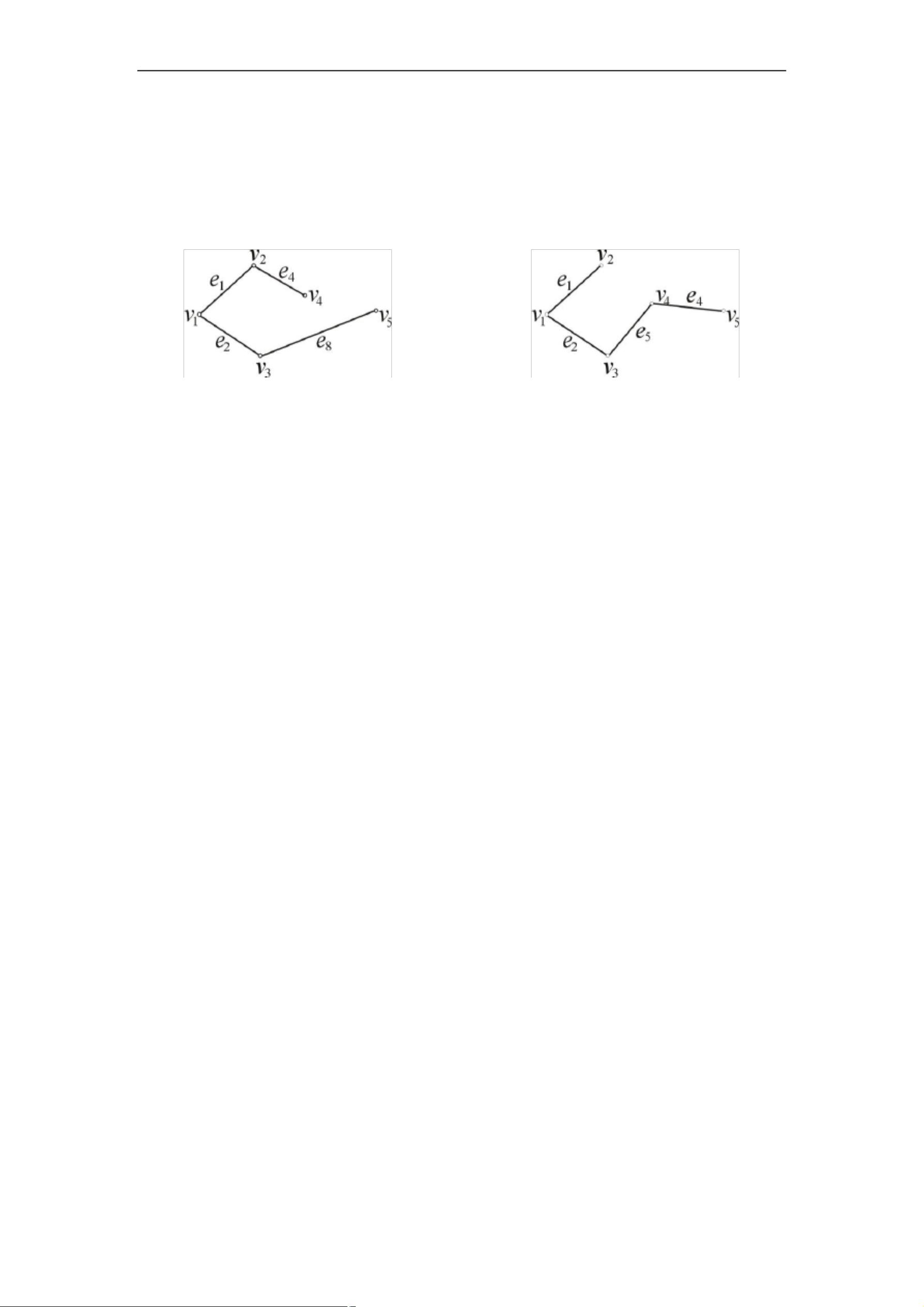
第六章介绍了最小生成树的概念及其性质。首先,树是一种特殊的图,它必须是连通的,即图中的任意两个顶点都通过一系列边相连,而且树中不存在环路。例如,电话线网络设计问题中,要确保所有城市之间都能通信,且边的数量最少,这就需要构建一个无环路的连通图,即树。
接着,定义了生成树。在任意一个图G中,如果能找到一个包含所有顶点的子图,且这个子图是一棵树,那么这个子图就被称为原图G的生成树。生成树保证了图的连通性,同时减少了边的数量。例如,大学的组织结构图,每个部门或单位可以看作一个顶点,上下级关系则表示边,整个结构形成一棵树,这棵树就是组织结构图的生成树。
最小生成树的概念引入了寻找图中权重最小的生成树的问题。定理6.1表明,一个图有生成树的充分必要条件是图本身是连通的。证明过程中,考虑了图是否含有环路的情况,通过删除环路中的边,可以构造出生成树,且这个过程可以重复进行,直到得到一个无环路的连通子图。
在实际计算最小生成树时,通常会使用算法,如Prim算法或Kruskal算法。Prim算法从一个顶点开始,逐步添加边,每次添加的边连接的是当前树与未加入树的顶点,且权重最小,直至覆盖所有顶点。Kruskal算法则是按边的权重排序,依次选择未导致环路的边加入生成树。
最小生成树模型在实际应用中具有很大的价值,比如在网络建设中,可以通过最小生成树模型来决定最经济的线路布局;在项目管理中,可以优化任务之间的依赖关系,降低成本。因此,理解和掌握最小生成树模型对于数据挖掘和计算机科学的专业人士来说至关重要。
2021-09-28 上传
2021-05-01 上传
2010-07-20 上传
2021-08-11 上传
2019-07-23 上传
2022-06-04 上传
G11176593
- 粉丝: 6874
- 资源: 3万+
最新资源
- MATLAB实现小波阈值去噪:Visushrink硬软算法对比
- 易语言实现画板图像缩放功能教程
- 大模型推荐系统: 优化算法与模型压缩技术
- Stancy: 静态文件驱动的简单RESTful API与前端框架集成
- 掌握Java全文搜索:深入Apache Lucene开源系统
- 19计应19田超的Python7-1试题整理
- 易语言实现多线程网络时间同步源码解析
- 人工智能大模型学习与实践指南
- 掌握Markdown:从基础到高级技巧解析
- JS-PizzaStore: JS应用程序模拟披萨递送服务
- CAMV开源XML编辑器:编辑、验证、设计及架构工具集
- 医学免疫学情景化自动生成考题系统
- 易语言实现多语言界面编程教程
- MATLAB实现16种回归算法在数据挖掘中的应用
- ***内容构建指南:深入HTML与LaTeX
- Python实现维基百科“历史上的今天”数据抓取教程