无符号数与有符号数：原码、补码、反码和移码解析

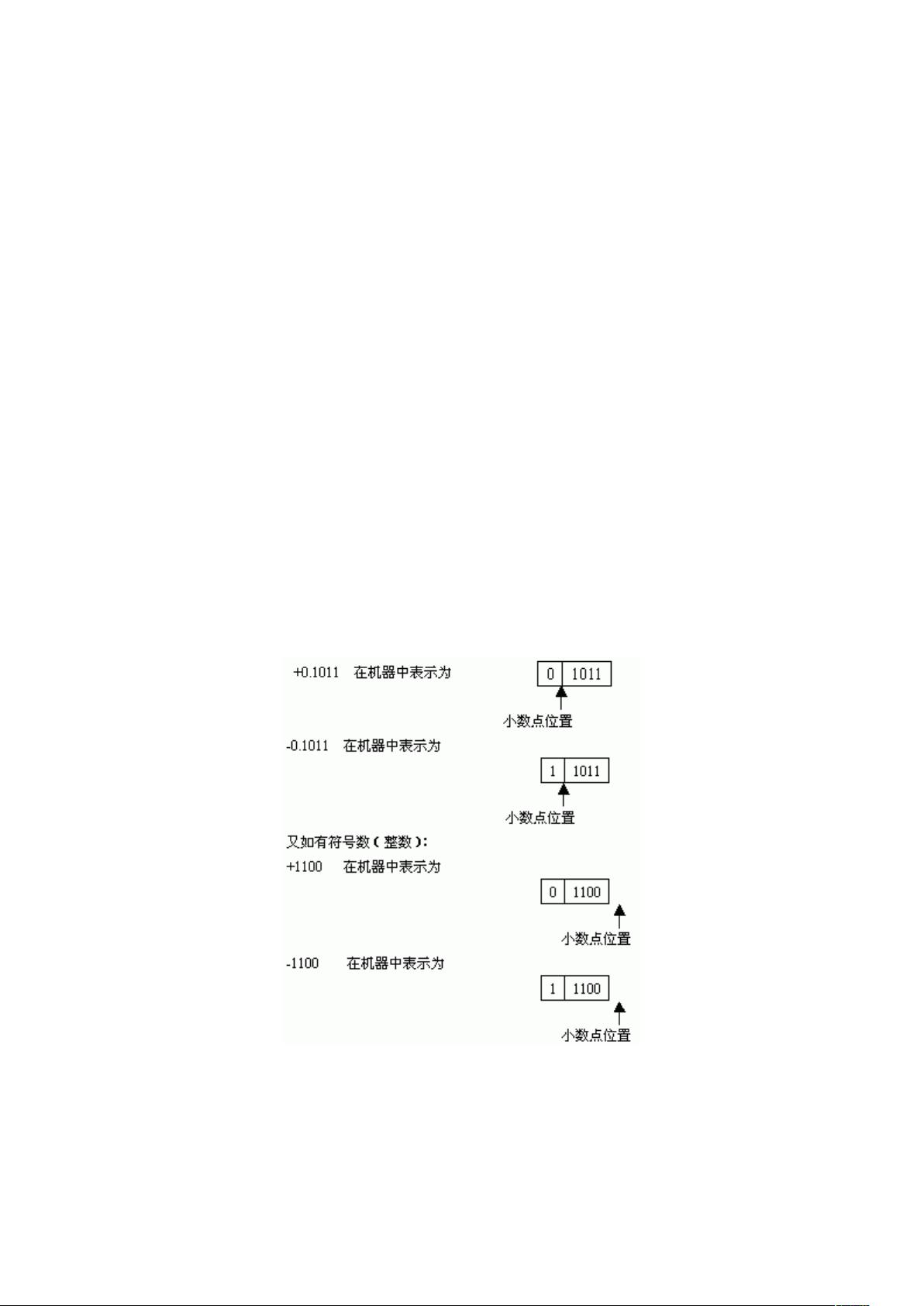
"本文主要介绍了计算机中无符号数和有符号数的概念，以及与之相关的机器数、真值、各种编码表示法，包括原码、补码、反码和移码。" 在计算机科学中，数据的存储和处理通常分为两类：无符号数和有符号数。无符号数顾名思义，是指没有附加符号的数字，其每一位都用来表示数值，因此在相同位数的机器字长下，无符号数可以表示更大的数值范围。例如，一个16位的无符号数可以表示从0到65535的整数，而同样的16位如果用于表示有符号数，其范围则变为-32768至+32767。 有符号数的处理则更为复杂，因为它需要区分正负。为了在计算机中表示正负，通常采用一种称为机器数的方式，其中最前面的一位用来表示符号，0代表正，1代表负。这种数字化的符号与数值结合形成了机器数，而我们日常生活中带有正负号的数值被称为真值。机器数的不同表示方法，如原码、补码、反码和移码，都是为了处理有符号数的运算问题。 原码是最直观的表示方式，它的符号位直接反映了数值的正负，数值位则对应真值的绝对值。对于整数，如果符号位为0，表示该数为正；若为1，则为负。例如，整数+1110的原码为0,1110，而-1110的原码为1,1110。对于小数，原码的表示方式类似，只是用小数点分隔符号位和数值位，如+0.1101的原码为0.1101，-0.1101的原码为1.1101。 原码虽然简单明了，但在处理负数的加减运算时会遇到问题，因为直接进行位运算会导致符号位的错误传播。为了解决这个问题，引入了补码、反码和移码等表示方法。补码是目前大多数计算机系统中用来表示有符号数的标准方式，它通过取反加1的方法确保了加法和减法运算的统一性。反码则主要用于中间计算过程，而移码常用于浮点数表示和浮点运算中，其符号位不变，其他位向左或右移位。 理解和掌握无符号数和有符号数及其表示方法是计算机底层原理的基础，这对于编程、硬件设计和系统级理解至关重要。在实际应用中，根据具体需求选择合适的编码方式，可以优化计算效率并减少错误的发生。