粒子滤波原理与MATLAB实现：对象追踪

"粒子滤波是一种用于估计动态系统状态的概率方法，通过使用一组随机样本来近似表示概率密度函数。这种技术尤其适用于非线性、非高斯的动态系统，其中传统的卡尔曼滤波可能不再适用。在物体跟踪等应用中，粒子滤波能有效地处理复杂环境下的不确定性。本文档将介绍粒子滤波的基本概念，并通过MATLAB实现来展示其工作原理。" 在算法开发过程中，MATLAB是一个强大的工具，尤其在进行对象跟踪时，如本示例中的粒子滤波应用。粒子滤波器（Particle Filter）的核心思想是使用一组随机样点（即“粒子”）在状态空间中分布，代表系统的后验概率分布。每个粒子都有一个权重，这个权重反映了该粒子表示真实状态的可能性。随着时间的推移，粒子通过预测和重采样两个主要步骤来更新。 首先，"预测"阶段基于系统模型对每个粒子的位置进行更新，这个模型通常是一个动态模型，例如微分方程，用来预测下一时刻的状态。然而，由于实际环境中的不确定性，预测结果可能存在误差。 接着，"重采样"阶段是粒子滤波的关键步骤。这一阶段依据粒子的权重重新生成新的粒子群体，使得高权重的粒子更有可能被保留下来，低权重的粒子则可能被替换。这样可以避免粒子群的退化，确保估计的准确性。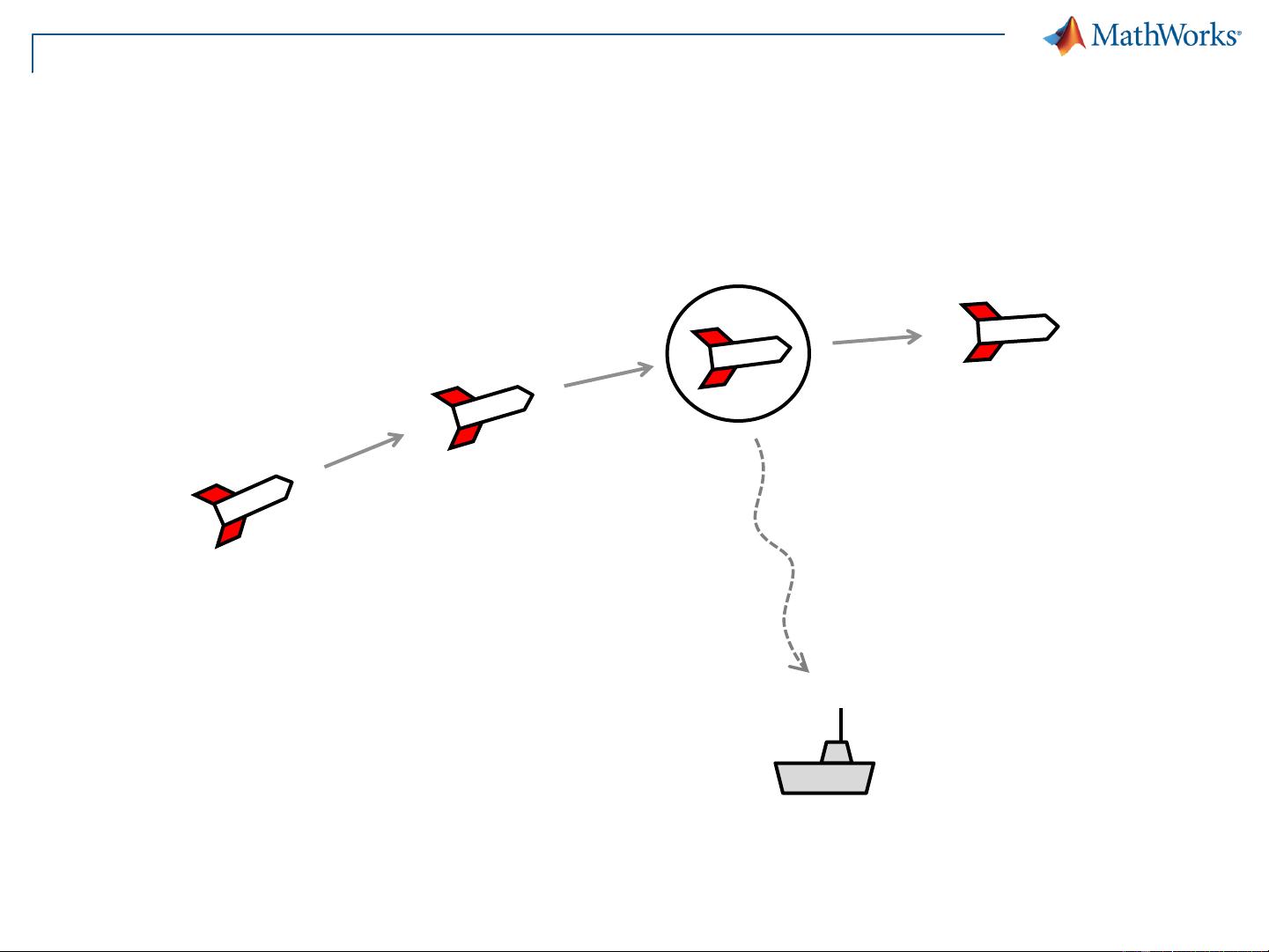 然而，粒子滤波面临两个主要问题。第一，长时间的模拟可能导致误差积累，影响估计的精度。第二，初始值的微小误差可能会导致解决方案的剧烈变化，这就是著名的蝴蝶效应。此外，单独依赖精确的预测或测量都无法理想地估计不可见或不可触碰的对象，例如火箭的轨迹。 因此，数据同化应运而生，它是结合预测和测量两种方法的统计技术。在粒子滤波中，这通常意味着在预测的粒子位置上应用观测信息，根据观测结果调整粒子的权重。通过这种方式，粒子滤波能够融合不完美的预测和测量，提供对未知或不可直接观测系统状态的估计。 粒子滤波是一种强大的工具，特别适合处理复杂的动态估计问题。通过MATLAB进行算法开发，可以直观地理解和实现这一技术，从而在诸如物体跟踪等领域实现高精度的状态估计。