1998-2012 NOIP历年普及组题目详解与解答

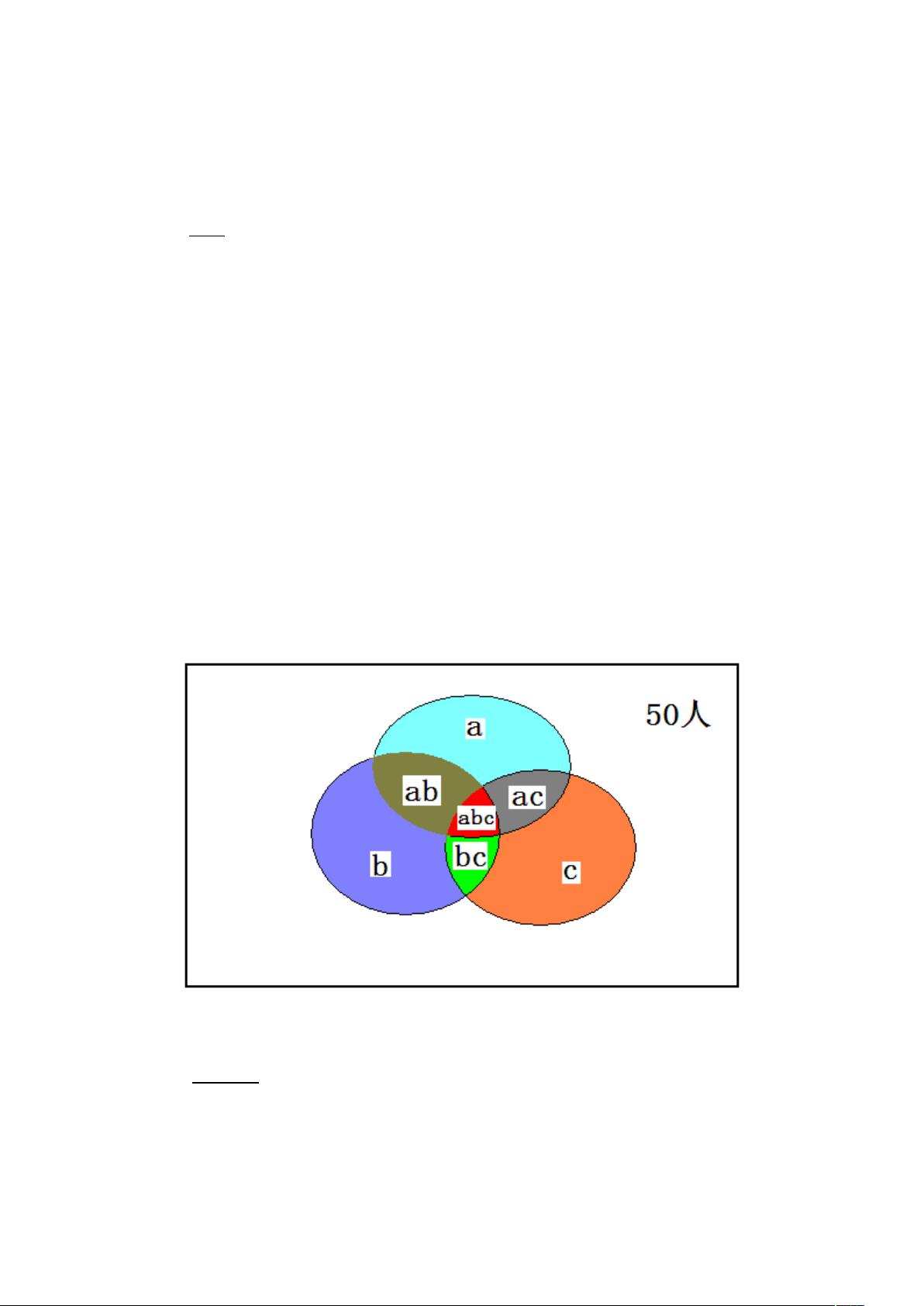
该资源是一系列NOIP（全国青少年信息学奥林匹克联赛）从1998年到2012年的普及组题目求解题解，涵盖了不同年度的数学和逻辑思维题目。以下是部分内容的详细解析： 1. 【1998年普及组】题目涉及数列理论，通过递推方程组解决。当给定特定的数列项a1=3, a2=-3, a3=1，求解满足特定规律的K值，即找到能使数列12^2, 22^2, ... 的系数和等于K^2的数列。通过尝试不同的K值并建立相应的方程组来找出整数解。 2. 题目要求计算阅读一本书的情况，涉及集合和逻辑推理。12个人至少读过一本书，而一本书被50人中30人未读过。通过分析给出的信息，计算出已读和未读人数的具体分布。 3. 在1999年的题目中，第一题要求学生分析一棵树的结构，利用入度和出度相等的性质，找出非根节点的总数。第二题则涉及到数论中的Nocomachns定理，即任何正整数的立方可以表示为连续奇数之和，通过给定示例推导出X与n的关系。 4. 2000年的问题包括组合数学和动态规划。第一题涉及五种不同形态的选择题，第二题考察斐波那契数列的定义，F(n)的递推公式为F(n) = F(n-2) + F(n-1)。 5. 2001年的题目混合了逻辑和计数技巧。第一题是关于选择满足特定条件的物品，第二题则是关于用若干点构成三角形的计数问题，区分了点在不同直线上的组合方式。 这些题目展示了NOIP普及组对基础数学、逻辑思维、数论和组合优化等方面的要求，对于准备参加NOIP的学生来说，理解和掌握这些题目的解法有助于提升他们的编程能力和问题解决能力。通过解决历年题解，学生可以了解比赛的常见题型和解题策略，为竞赛做足准备。