B-M算法示例：序列密码生成与分解

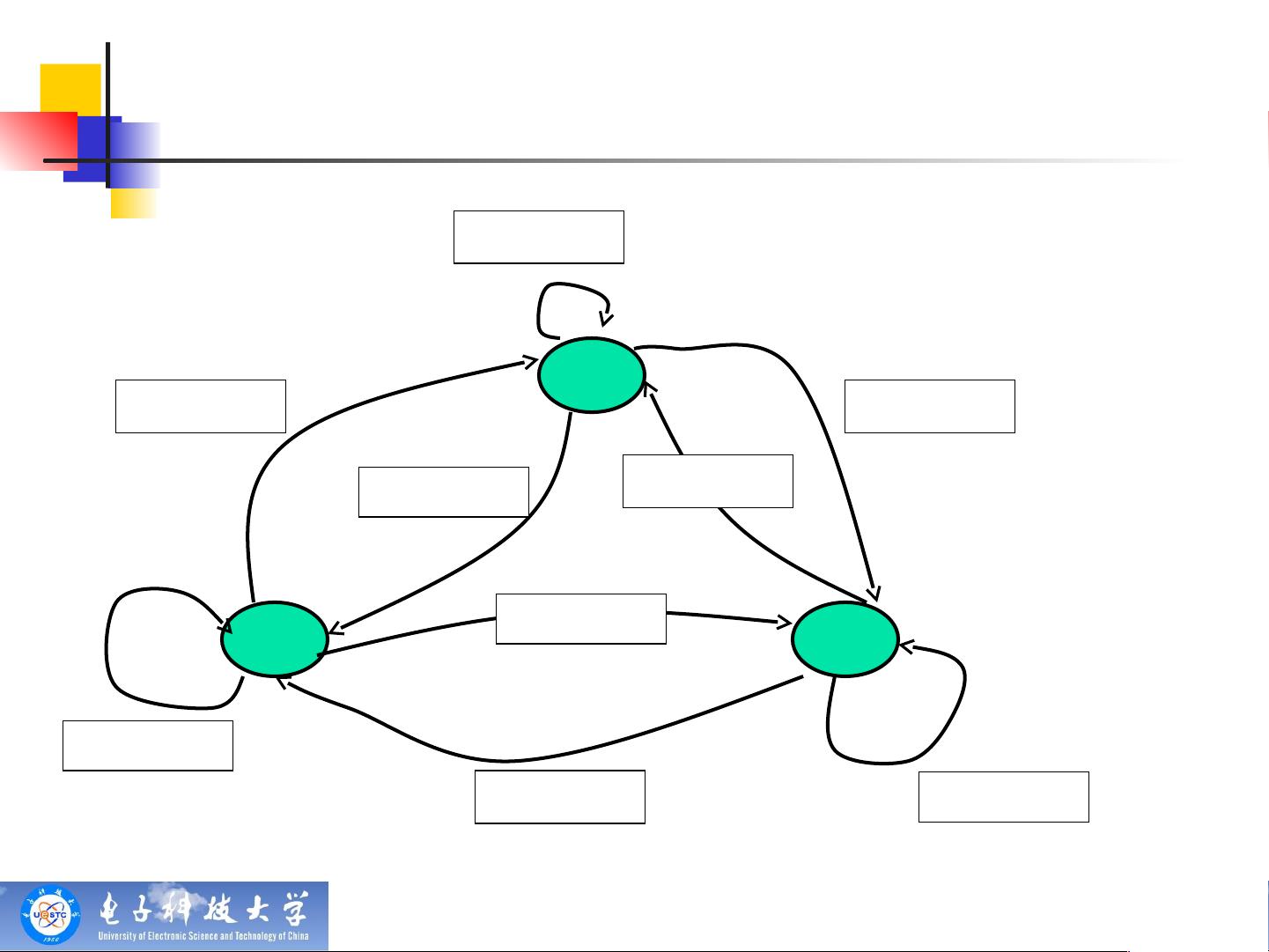
本文主要探讨了应用B-M算法在序列密码中的实例。序列密码是一种基于密钥流生成技术的加密方式，其中的核心思想是利用密钥k生成一个无限或有限长度的密钥流z，然后通过特定的加密规则将明文转换成密文。文章以具体例子来解释这一过程： 首先，作者举了一个简单的例子，其中明文"rendezvous"被转换为整数序列17413342521142018，使用密钥K=8生成的密钥流为81741334252114。这个密钥流再应用于每个明文字符进行异或（XOR）操作，生成的密文对应整数序列为2521171673209812，最终表现为"zvrqhdujim"。 同步序列密码是文中重点介绍的类型，因为其密钥流生成器（滚动密钥生成器）仅依赖于密钥k和当前状态σi，而不受输入明文的影响。这种设计使得密文yi不依赖于先前的明文字符，因此可以将加密过程分解为密钥流生成和加密变换两部分。同步序列密码的加密和解密过程可以通过如下的模型表示： 加密器结构： 1. 密钥流生成器：zi = f(k, σi) 2. 加密变换器：yi = Ez(xi)，这里的E通常为XOR或其他简单的算术运算 解密器结构： 1. 密钥流生成器保持不变：zi = f(k, σi) 2. 解密变换器：xi = Dzi(yi)，D是与加密变换对应的逆运算，恢复原始明文。 B-M算法在这里可能指的是伯努利多项式生成器（Berlekamp-Massey algorithm），一种用于寻找最小多项式来重构序列密码密钥流生成器的算法。通过B-M算法，可以从有限长度的密钥流样本中恢复出最简形式的线性反馈移位寄存器（LFSR）的生成多项式，从而破解同步序列密码。 本文通过实际示例和理论讲解，深入剖析了同步序列密码的工作原理，以及如何运用B-M算法来分析和解码这类密码系统。这对于理解序列密码的构造、加密和安全性评估具有重要意义。