模拟退火算法详解与应用

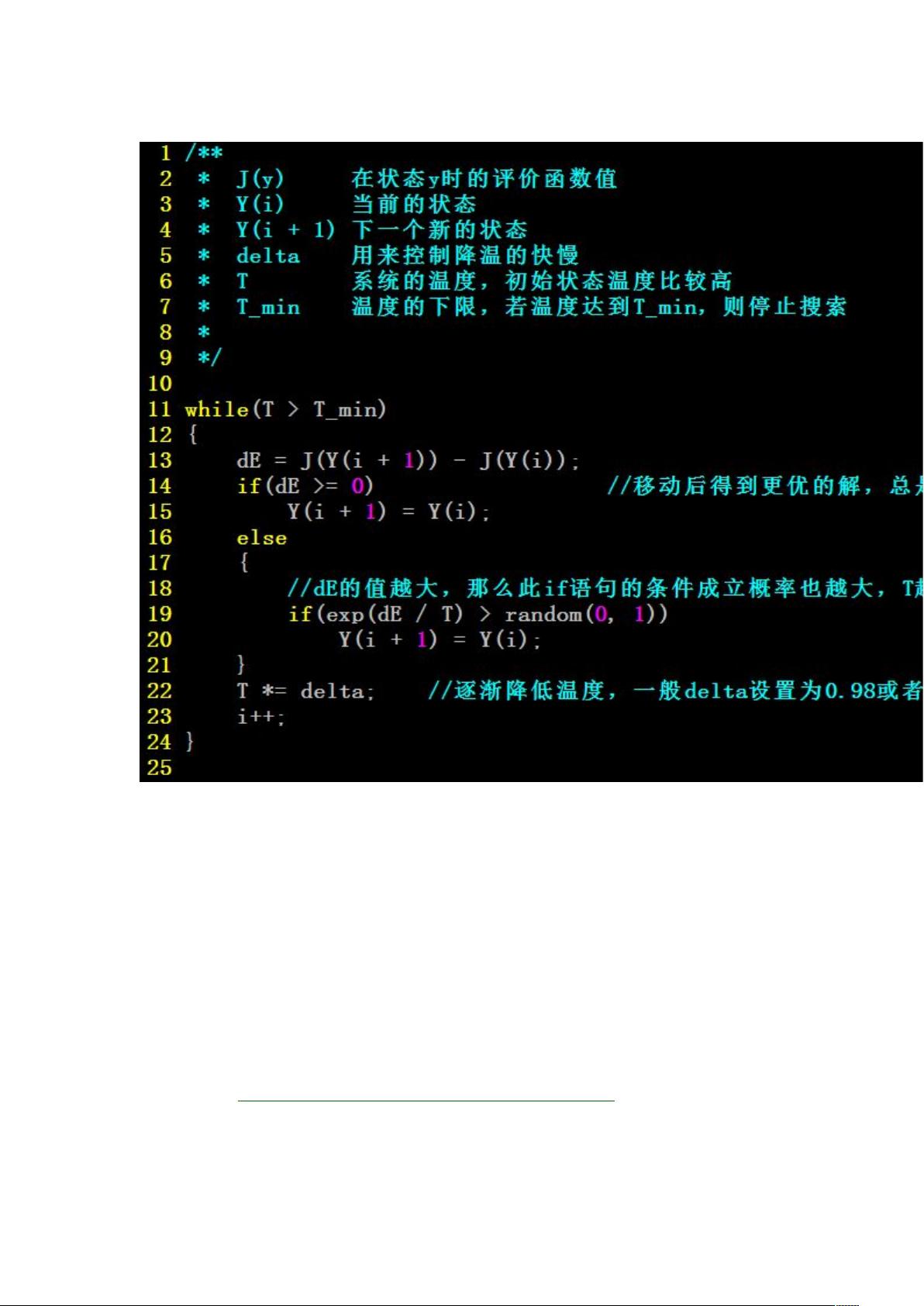
"模拟退火算法是一种用于解决NP完全优化问题的算法，它能有效地避免局部最优解。这种算法借鉴了物理学中固体退火的过程，通过逐步降低温度来寻找全局最优解。在模拟退火算法中，初始设置一个较高的温度，然后随着时间的推移，温度逐渐降低，直到达到一个低温状态，此时目标函数达到最小值。算法的核心在于它允许在一定概率下接受比当前解更差的解，以增加探索全局最优解的可能性。 1. 模拟退火算法认识 模拟退火算法与爬山算法类似，但更具有全局视野。在爬山算法中，我们总是选择使得目标函数增大的方向移动，而在模拟退火算法中，即使新的状态导致目标函数增大，也有可能被接受，这取决于当前的温度和两个状态之间的能量差。这种随机性使得算法能够在局部最优解附近进行探索，有可能跳到全局最优解。 2. 模拟退火算法描述 算法的关键在于接受更差解的概率函数，通常用指数函数表示，这个概率随着温度的降低而迅速减小。如果新状态的能量（即目标函数值）低于当前状态，则总是接受这个变化；反之，如果新状态的能量更高，则以P(dE)的概率接受，其中P(dE) = exp(-dE/T)，dE是能量差，T是当前温度。这个概率公式保证了在高温时更容易接受差的解，低温时更倾向于保留好的解。 3. 应用实例 - 费马点问题：这是一个经典的几何问题，要求找到一个点，使得该点到给定n个点的距离之和最小。模拟退火可以用来寻找这个问题的近似解。POJ 2420题给出了具体的实现，通过迭代和温度控制，找到满足条件的点。 4. 其他应用 - 最小包含球问题：寻找一个球，使得所有点都位于球内或球面上，以最小化球的半径。模拟退火可以用来调整球心位置，逐渐优化半径。 - 函数最值问题：对于复杂函数，寻找极大值或极小值，模拟退火可以通过在函数空间中随机移动并根据温度决定是否接受新解，以找到全局极值。 - 旅行商问题（TSP）：经典的组合优化问题，模拟退火可以生成接近最优的旅行路线，通过不断调整城市访问顺序并根据温度决定是否接受更长的路线。 模拟退火算法的效率和精度取决于初始温度、降温速率以及迭代次数等参数的选择。在实际应用中，需要对这些参数进行合理设置，以保证算法既能充分探索解决方案空间，又能避免过多的计算成本。模拟退火是一种灵活且强大的优化工具，尤其适用于解决复杂问题的全局优化。