"树tree的定义及二叉树遍历"

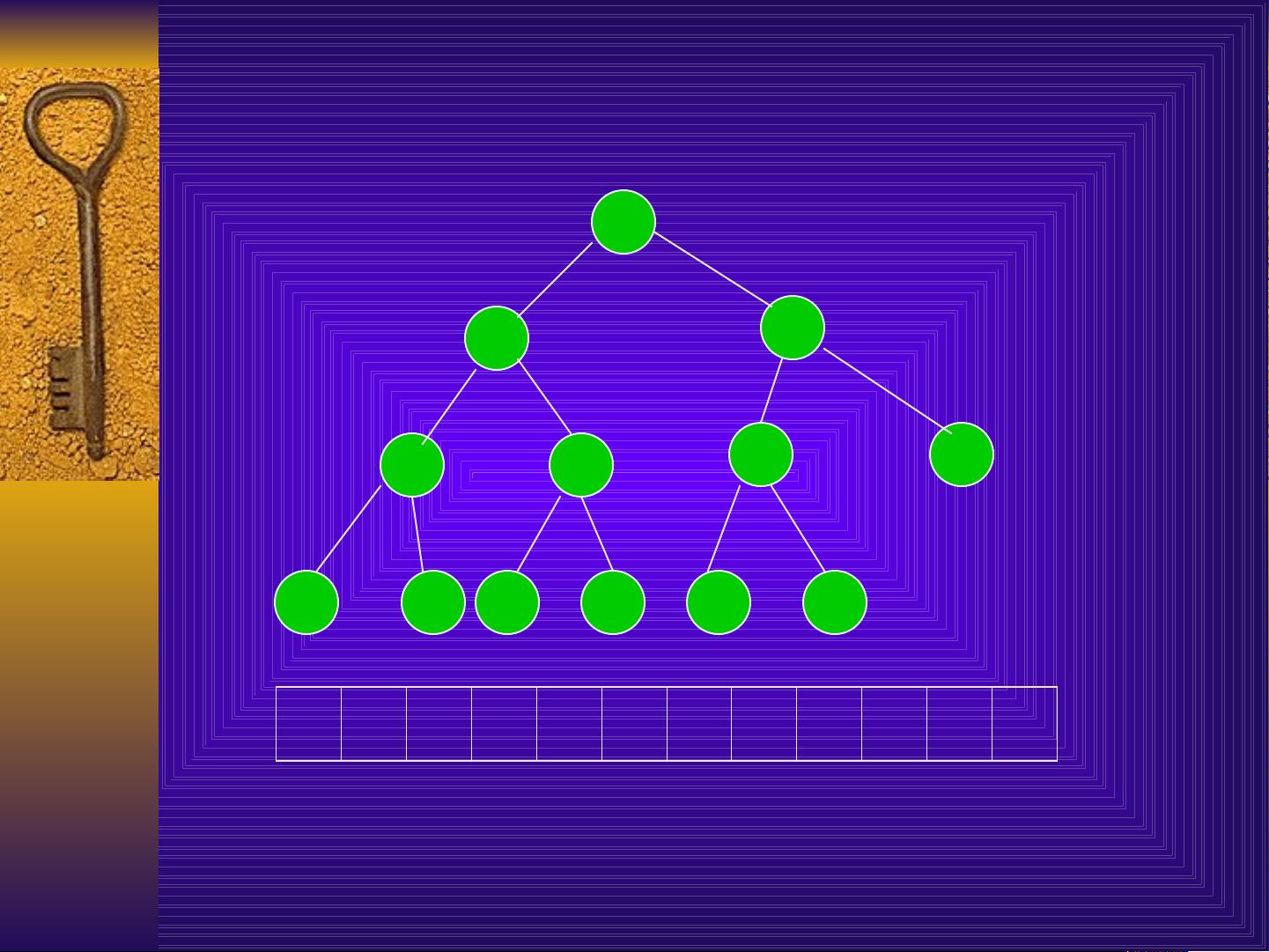
数据结构【二叉树】是一个包含根结点和若干子树的树结构。其中，根结点是唯一的，其余结点根据子树的不同而互不相交。树可以进一步细分为二叉树，在二叉树中，每个结点最多有两个子结点。 在二叉树的操作中，常见的有二叉树遍历、线索二叉树、二叉搜索树、二叉树的计数、堆、树与森林、霍夫曼树等。 二叉树的遍历指的是按照一定顺序访问二叉树中的所有结点。常见的遍历方式有前序遍历、中序遍历和后序遍历。 前序遍历是指先访问根结点，然后按照先左后右的顺序依次遍历左子树和右子树。中序遍历是指在根结点之前先遍历左子树，然后访问根结点，最后再遍历右子树。后序遍历是指先遍历左子树，然后再遍历右子树，最后访问根结点。 线索二叉树是对二叉树进行了优化的一种数据结构。在线索二叉树中，每个结点都包含指向其前驱结点和后继结点的指针，这样可以直接访问二叉树中某个结点的前驱和后继结点，而无需遍历整个树。 二叉搜索树又称有序二叉树，它是一棵特殊的二叉树，其中每个结点的值都大于其左子树中的任意结点的值，小于其右子树中的任意结点的值。这样的特性使得在二叉搜索树中进行搜索、插入和删除等操作更加高效。 二叉树的计数是指统计一个给定结点数的二叉树有多少种不同的结构。这个问题可以使用动态规划的方法来解决，根据不同的根结点和左右子树的结构，逐步递推出给定结点数的二叉树的个数。 堆是一种特殊的二叉树结构，其中每个结点的值都大于（或小于）其子结点的值。堆分为大顶堆和小顶堆，用于实现优先队列等数据结构。 树与森林是一种多个树结构的组合，每个子树都是一棵独立的树。树和森林可以通过遍历和其他操作进行处理。 霍夫曼树是一种带权路径最短的二叉树。在霍夫曼树中，每个叶子结点都表示一个字符，而每个非叶子结点都表示一个字符的编码。通过构建霍夫曼树可以实现无损压缩等应用。 总之，数据结构【二叉树】是一种由根结点和若干子树组成的树结构。在二叉树的操作中，常见的有二叉树遍历、线索二叉树、二叉搜索树、二叉树的计数、堆、树与森林、霍夫曼树等。这些操作和数据结构可以在实际的编程和算法设计中发挥重要作用。