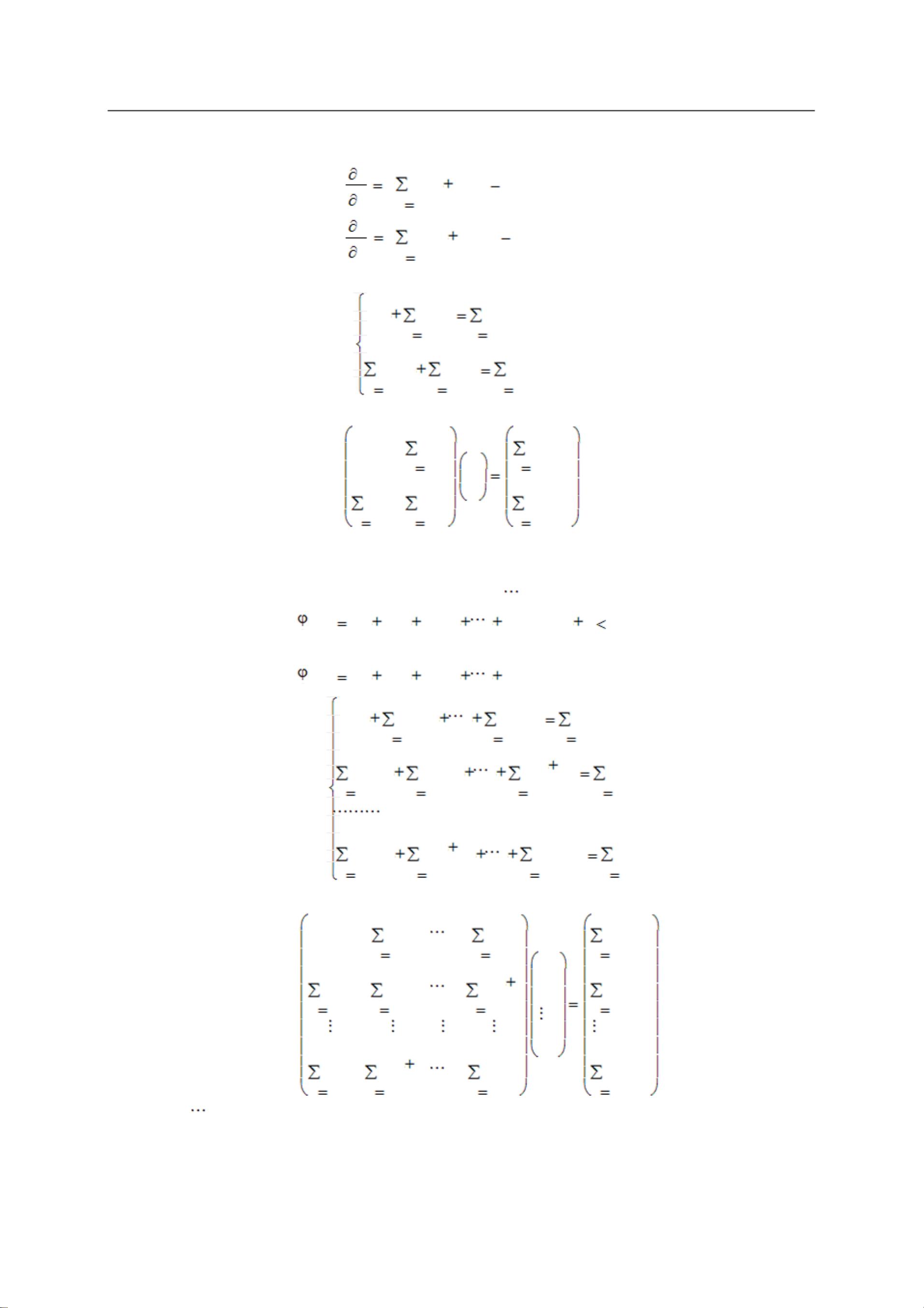分段曲线拟合新方法：实现连续与光滑的Hermite插值

"分段曲线拟合方法研究，利用R语言实现自动分段拟合，通过两点三次Hermite插值确保分段点连续性" 在数据处理领域，分段曲线拟合是一种常见的技术，用于将离散数据点近似地表示为连续曲线。这种方法尤其适用于数据分布具有多个局部特征或趋势变化的情况。然而，传统的分段曲线拟合方法往往在分段点处存在不连续性和不光滑的问题，这可能导致拟合结果失真，影响数据分析的准确性。 针对这个问题，本文提出了一种改进的分段曲线拟合策略，该策略充分利用R语言的强大功能来自动化这个过程。R语言是一种广泛应用于统计分析和图形绘制的编程语言，拥有丰富的库和工具，非常适合进行曲线拟合和数据处理任务。 具体来说，该方法分为以下步骤： 1. 分段曲线拟合：首先，使用R语言对数据进行初步的分段曲线拟合，通常会选择不同的多项式函数（如线性、二次或更高阶）来适应各个数据子集的趋势。 2. Hermite插值：在相邻的两个拟合曲线段之间，采用两点三次Hermite插值法。这种方法基于四个控制点（两个端点以及它们的一阶导数信息）来构建一条三次曲线，使得新曲线不仅连接了两个分段点，而且保证了在这些点的一阶导数连续，从而实现了整体的连续性和光滑性。 3. 连续性保证：通过这种方式，即使数据点在分段点附近有突变，也可以得到平滑的过渡，避免了拟合曲线的不连续性。这有助于提高拟合的质量，使分析结果更加可靠。 4. 实例验证：通过几个实际案例，文章展示了该方法在不同数据集上的应用，证明了其简单易用、实用性高且效果良好。 关键词中的“Hermite插值”是指一种基于数据点及其导数信息的插值方法，它能够更好地保持数据的局部特性，尤其是在处理需要保持光滑性的曲线拟合时。而“分段点连续”则强调了这个方法的关键目标，即确保拟合曲线在各段间的连续性。 这种分段曲线拟合方法结合了R语言的编程优势和Hermite插值的数学特性，为处理复杂数据提供了有效且精确的工具，对于数据科学家和工程师来说具有很高的实用价值。在处理大量数据并需要精确描述数据趋势时，这种方法尤其有用，因为它可以在保证计算效率的同时，减少由不连续性引起的误差。