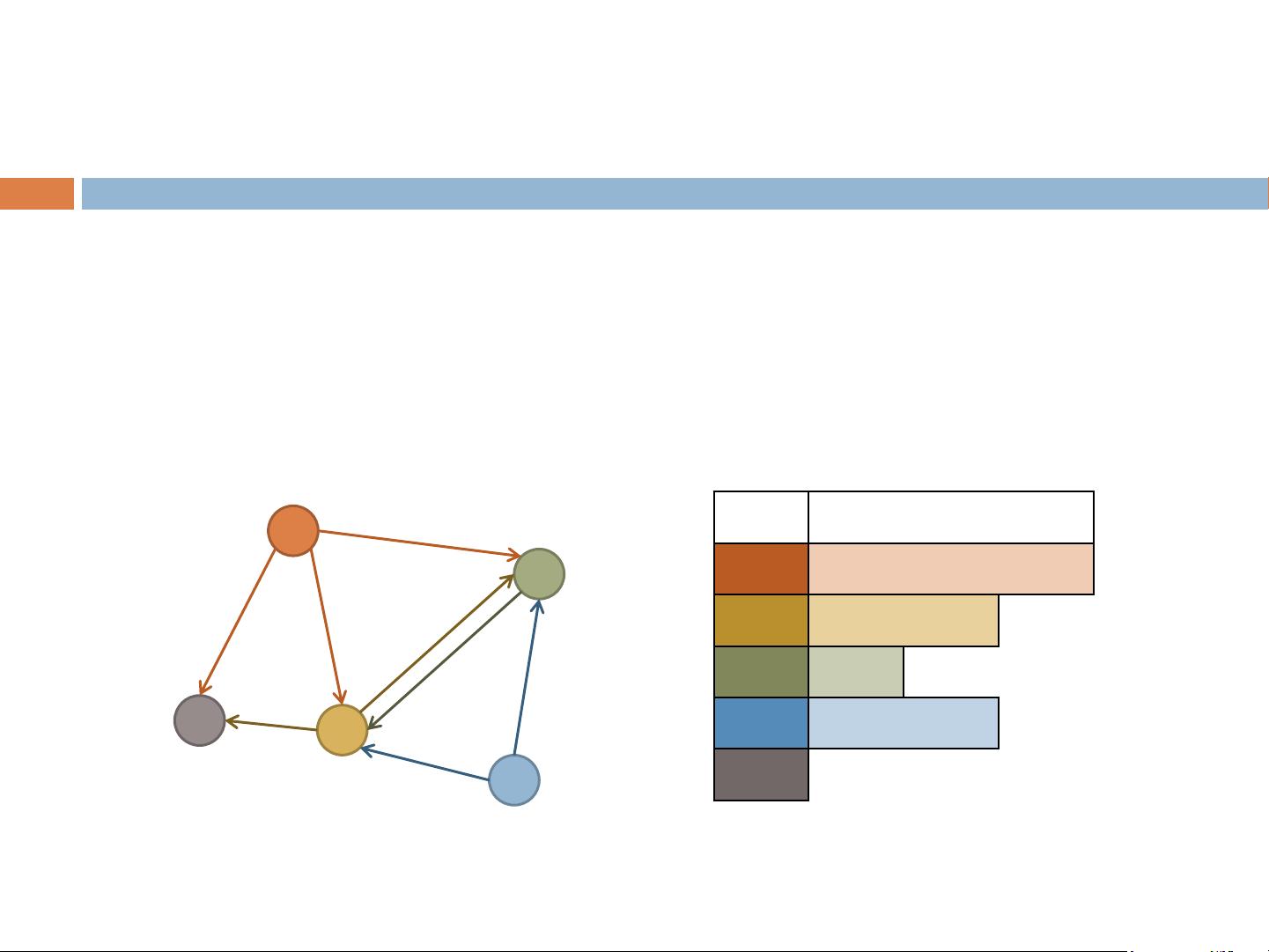
图论基础：邻接矩阵与邻接表存储

在本篇关于图论算法的讲解中，我们将探讨图形的基本概念、数据结构表示以及它们在实际问题中的应用。首先，我们会介绍什么是图，它是一种抽象的数据结构，由节点（或顶点）和连接这些节点的边组成。为了便于讨论，我们通常会给节点编号，从1到n，而边可以是单向（有向）或双向。节点和边可以附带额外的信息，如权重或方向。 学习图论的原因在于，许多现实世界的问题都可以通过图形来表述和解决。这些问题包括但不限于： 1. **最短路径问题**：寻找两个节点之间的最短路径，例如Dijkstra算法和Floyd-Warshall算法。 2. **网络流问题**：在图中分配流量以满足特定条件，如Ford-Fulkerson算法。 3. **匹配问题**：确定图中最大可能的一对节点没有共同邻居的边，如霍夫曼树和最大独立集。 4. **2-SAT问题**：逻辑推理中的一个经典问题，可转化为求解有向图的可行性。 5. **图着色问题**：最少颜色着色图使得相邻节点颜色不同，涉及分治和启发式搜索。 6. **旅行商问题（TSP）**：寻找访问所有节点恰好一次的最短路径，至今仍然是未解决的难题。 在存储图时，我们需要处理节点集𝑉和边集𝐸。常见的方法是使用数组存储节点，对于边的存储，一种常见方式是使用邻接矩阵（Adjacency Matrix），其中每个元素表示对应节点之间的边是否存在。然而，邻接矩阵占用空间较大，特别是对于稀疏图，邻接列表（Adjacency List）更高效，它用链表形式存储每节点的邻接边，支持快速查找和添加/删除操作。 邻接列表支持以下操作： - **查询给定节点的所有邻接边**：通过遍历节点对应的链表实现。 - **测试两个节点是否相连**：直接检查链表中的对应位置即可。 深度优先搜索（DFS）和广度优先搜索（BFS）是图搜索的两种基本策略，用于遍历图或寻找特定路径。深度优先搜索通常用于找到任意两点之间的路径，而广度优先搜索更适合于寻找最短路径。 接下来，我们会讨论图的拓扑排序，它是有向无环图（DAG）中的一种排列，节点的顺序符合依赖关系。此外，讲解的重点还会涉及欧拉回路（Eulerian Circuit）和最小生成树（Minimum Spanning Tree，MST），前者是可以在图中形成一个回路且经过每条边恰好一次的路径，后者则是连接所有节点且总长度最小的边集合。 最后，我们会涉及强连通分量（Strongly Connected Components, SCC），这是图论中的一个重要概念，用于划分图中可以互相到达的节点集合，对于某些问题如程序分析和系统设计有着重要作用。 这堂课涵盖了图论基础概念、数据结构及其应用，旨在帮助理解这些工具如何解决实际问题，并为后续深入研究提供坚实的基础。无论是算法设计还是实际工程应用，图论都是计算机科学中不可或缺的一部分。