图的数据结构详解：遍历、连通性、最小生成树与最短路径

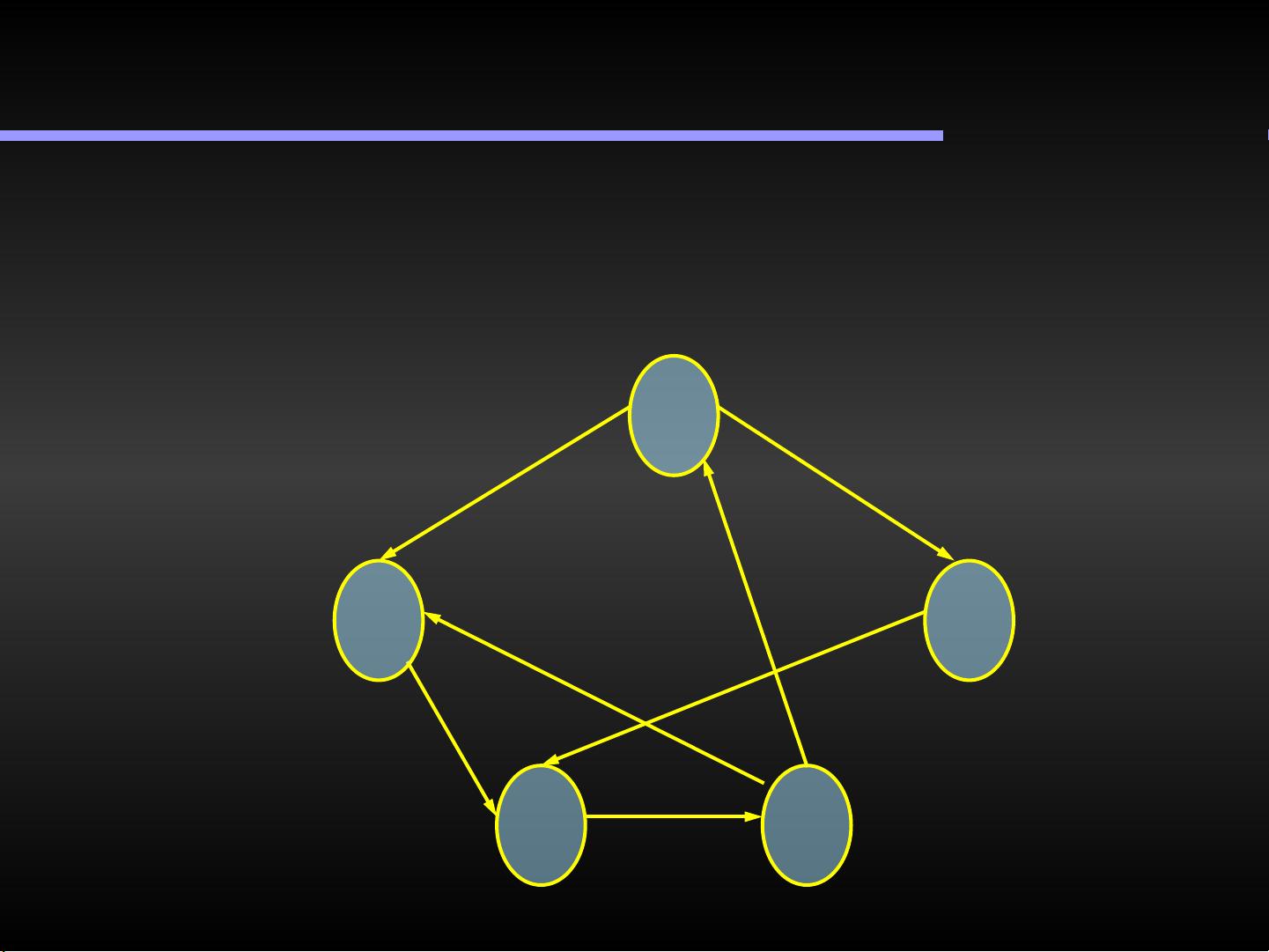
"图的内容讲解，涵盖图的基本概念、存储结构、遍历方式、连通性、最小生成树和最短路径等核心知识点。" 在数据结构中，图是一种非常重要的抽象数据类型，用于表示对象之间的关系。图由顶点（或节点）和边（或连接）构成，能够用来描述各种复杂的关系网络。根据描述和标签，我们将深入探讨以下几个方面： 1. **图的基本概念** - 图由顶点集合V和边集合E组成，通常表示为Graph=(V,E)。 - 顶点可以代表任何数据对象，而边表示顶点间的关系。 - 边可以是有向的（<x,y>，表示从x到y的方向）或无向的（(x,y)，没有特定方向）。 - 混合图同时包含有向边和无向边。 2. **图的存储结构** - 邻接矩阵：一个二维数组，其中的元素表示对应顶点间是否有边相连。对于有向图，邻接矩阵是对称的；对于无向图，它是对称的且半正定。 - 邻接表：每个顶点都有一个链表，链表包含与其相邻的所有顶点。适用于节省空间，特别是当图稀疏时。 3. **图的遍历** - 广度优先搜索(BFS)：从起始顶点开始，逐层访问所有相邻顶点，通常用于查找最短路径或确定图的连通性。 - 深度优先搜索(DFS)：从起始顶点开始，尽可能深地探索图的分支，通常用于发现回路或拓扑排序。 4. **图的连通性问题** - 连通图：图中的任意两个顶点都通过边可以直接或间接相连。 - 强连通图：对于有向图，如果每对顶点之间都存在双向的路径，则该图是强连通的。 - 生成树：图的一个子集，包含了原图的所有顶点，且任意两个顶点间仅有一条路径，无环。 5. **最小生成树** - 在加权图中，寻找一个边的集合，这些边连接了所有顶点并且总权重最小，这个集合就被称为最小生成树。常见的算法有Prim算法和Kruskal算法。 6. **最短路径** - 在带权重的图中，寻找两个顶点间路径的最小权重。Dijkstra算法常用于找到单源最短路径，Floyd-Warshall算法则可以找到所有顶点对的最短路径。 7. **活动网络** - 在图中，顶点代表事件，边代表活动，边上的权重代表活动所需的时间。这种图常用于项目管理，如关键路径分析(CPA)和计划评审技术(PERT)。 图的概念广泛应用于计算机科学的各个领域，如网络路由、社会网络分析、生物信息学、软件工程等。理解并掌握这些基本概念和算法对于解决实际问题至关重要。通过实例，例如交通图、电路图、通讯线路图和流程图，我们可以看到图在模拟现实世界问题中的强大能力。