Python二分查找与算术平方根算法详解

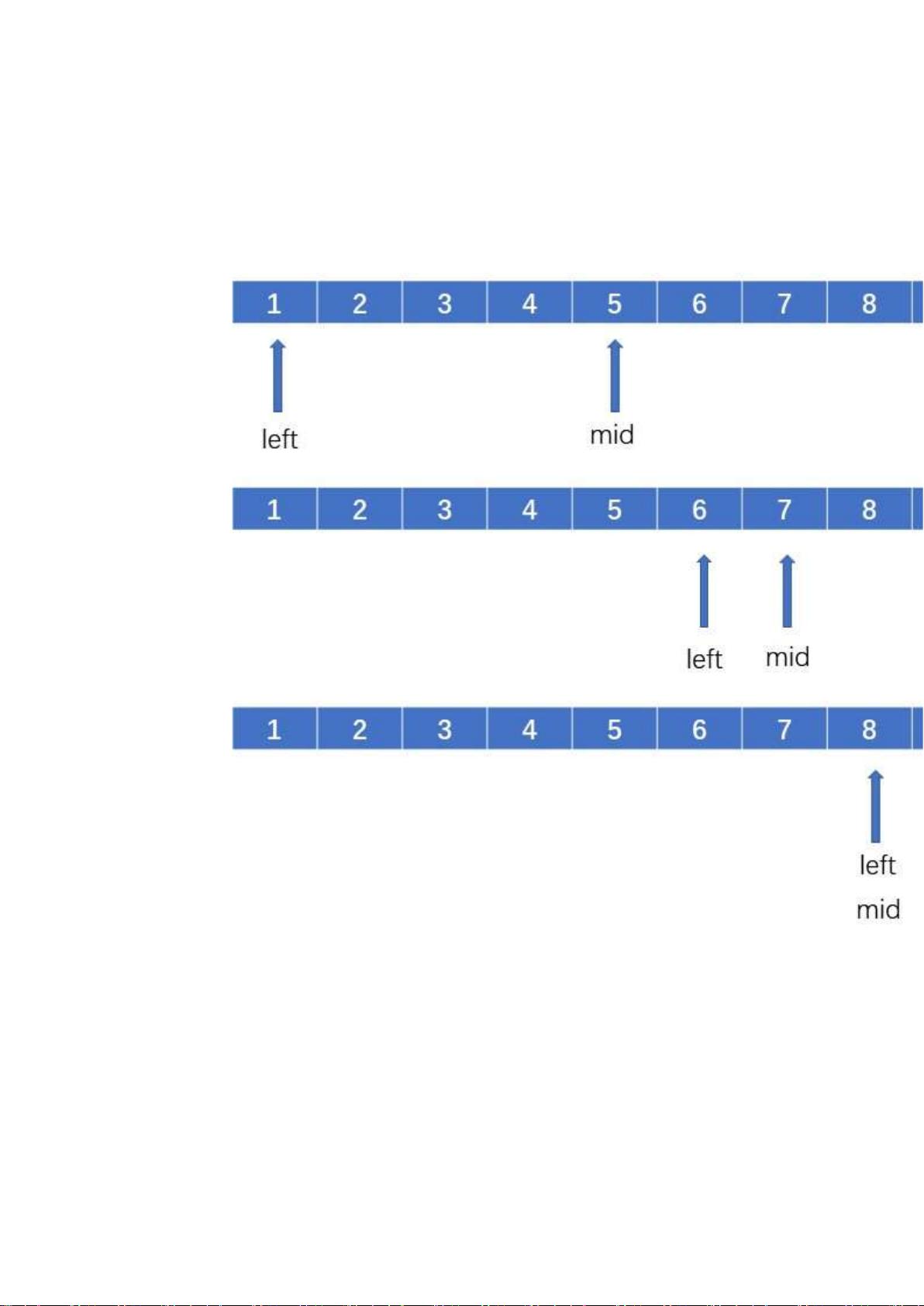
二分法是一种高效的搜索算法，尤其适用于有序数据的查找。在编程中，它通常用于在已排序的数组或列表中寻找特定元素的位置。本文档主要介绍了如何使用Python实现二分查找法解决两个力扣（LeetCode）问题。 首先，力扣问题704是关于在一个已排序的整型数组`nums`中查找目标值`target`的索引。在这个问题中，定义了一个名为`Solution`的类，其中包含两个方法。第一个方法`search`使用传统的二分查找逻辑： 1. 初始化左边界`left`为0，右边界`right`为数组长度减1。 2. 在`while`循环中，计算中间索引`middle`，确保不会发生整数溢出。 3. 比较目标值与中间元素`nums[middle]`： - 如果`nums[middle]`大于`target`，说明目标在左半部分，更新右边界为`middle-1`。 - 如果`nums[middle]`小于`target`，说明目标在右半部分，更新左边界为`middle+1`。 - 当找到目标值时，返回`middle`；否则，循环结束后返回-1表示未找到。 第二个方法是一个“抖机灵”的版本，利用Python的内置特性`in`检查目标值是否直接存在于数组中，如果存在，则返回其索引，否则返回-1。 接下来，力扣问题69要求计算非负整数`x`的算术平方根，并且不能使用内置的指数运算。这个问题使用了二分查找的思想，但并非在数组中查找，而是在一个特定范围内找到一个数，该数的平方等于`x`。算法步骤如下： 1. 初始化左边界`left`为0，右边界`right`为`x`。 2. 在`while`循环中，同样避免溢出地计算中间值`mid`。 3. 判断`mid*mid`与`x`的关系： - 如果`mid*mid`大于`x`，说明实际平方根应该在`mid`的左半部分，即`left=mid-1`。 - 如果`mid*mid`小于`x`，说明实际平方根在`mid`的右半部分，即`right=mid+1`。 4. 当找到满足条件的`mid`（即`mid*mid == x`），返回`mid`作为结果，因为题目要求整数部分。 二分法之所以高效，是因为每次迭代都将搜索范围缩小一半，对于大规模数据，其时间复杂度为O(log n)，比线性搜索（O(n)）要快得多。掌握二分查找不仅能够解决这类问题，还能应用于更广泛的场景，如在排序算法、数据压缩、数据库查询等优化中。