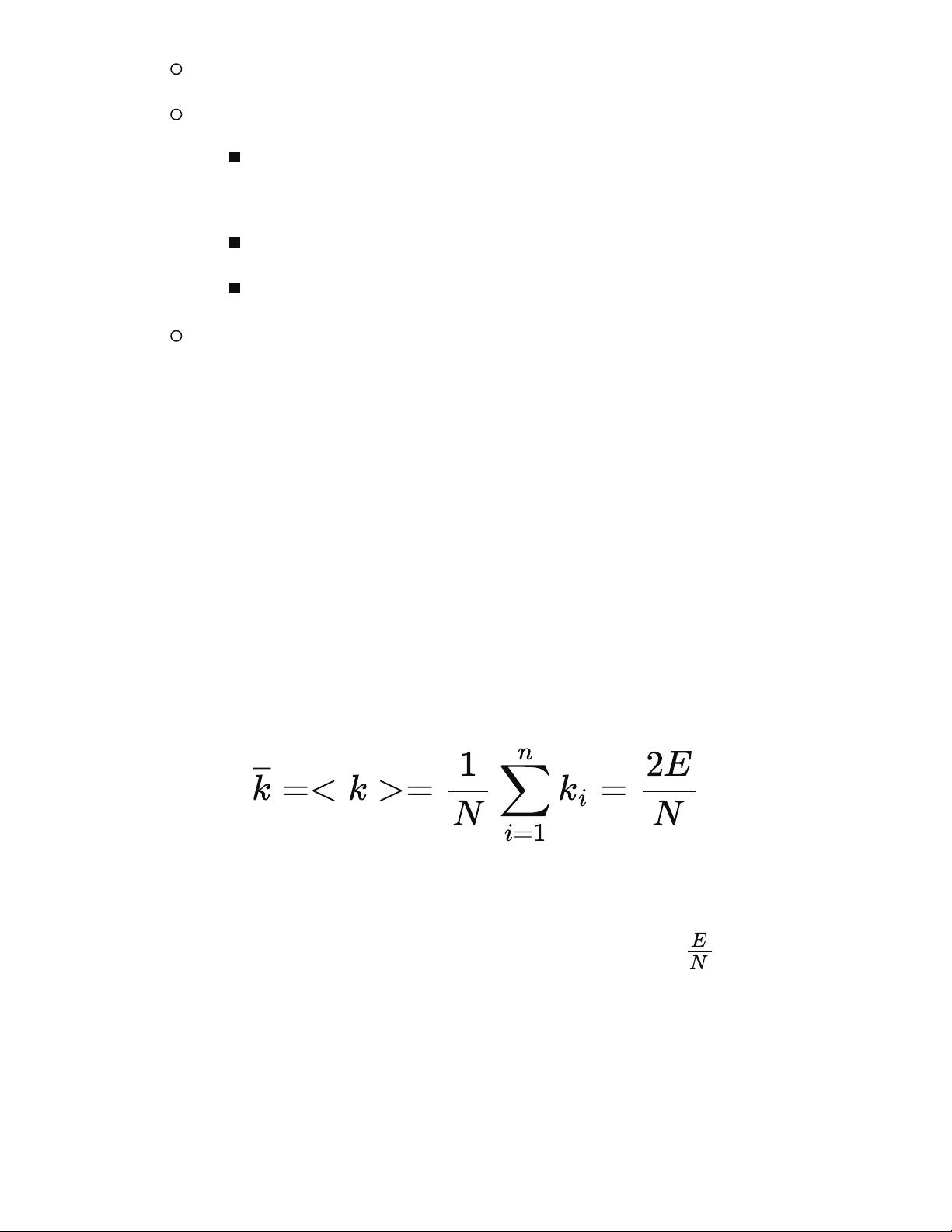
图机器学习：图的基本表示与特征工程【深入解析本体设计与数据关系】

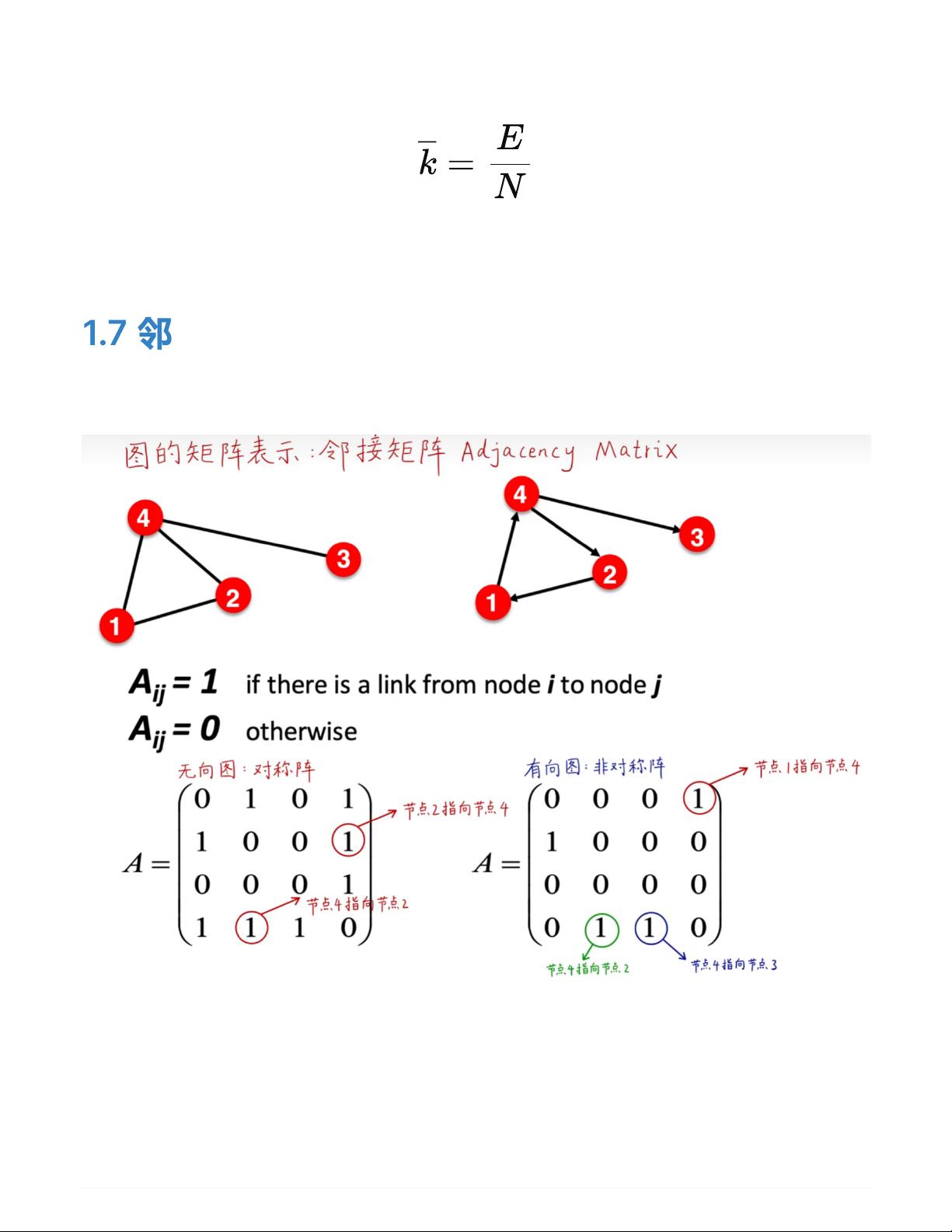
图机器学习第二章主要围绕图的基本表示与特征工程展开。首先介绍了图的基本表示，包括图的种类（有向、无向、异质、二分、连接带权重）以及节点和连接的基本组成。图可以用节点和连接组成，节点也可以称为vertices或者nodes，连接也可以称为edges或者links，整个图可以被表示为G(N,E)。在图的基本表示中，有三种常用的表示方法，分别是邻接矩阵、连接列表和邻接列表。邻接矩阵适用于稠密图，通过矩阵来表示节点之间的连接关系；连接列表则适用于稀疏图，通过列表的形式存储每个节点的连接情况；而邻接列表则是连接列表的一种变体，更加高效地表示图的连接结构。 在图的组成成分中，其实图的表示方式是可以灵活变化的。以一个具体例子来说，我们可以将某个场景中的数据设计成图，当需要导航时，路段可以作为节点，而路段之间的连通性则可以作为连接。但是当换一个角度看待这个场景时，我们也可以将地点作为节点，这样路段就会变成连接。因此，面对不同的数据，我们需要根据具体的场景来决定哪些数据应该被当作节点，哪些数据应该被当作连接。这就引出了本体图的概念，本体图（Ontology）可以事先定义好数据之间的关系，比如食物与疾病之间的关系，这一步在导入数据之前就需要进行设计。当具体的数据导入之后，实体变成了图中的节点，而连接则变成了连接节点之间的关系。 除了图的基本表示之外，第二章还介绍了特征工程在图机器学习中的重要性。特征工程在传统的机器学习任务中已经被广泛应用，而在图机器学习中，不同的图结构需要不同的特征提取方法。由于图的结构复杂，节点和连接之间存在多种关系，因此如何提取有效的特征是一个具有挑战性的问题。常见的特征提取方法包括节点的度、节点的邻居信息、节点之间的路径以及子图结构等。此外，图嵌入（Graph Embedding）也是一种重要的特征提取方法，它可以将图中的节点或者连接映射到低维空间中，从而方便后续的机器学习模型进行处理。 总的来说，图机器学习第二章深入探讨了图的基本表示与特征工程，强调了在处理图数据时需要事先设计好数据之间的关系，并结合合适的特征工程方法来提取有效的特征。通过对图的基本表示和特征工程的深入理解，我们可以更好地应用图机器学习技术解决现实世界中的复杂问题。