使用幂法计算矩阵主特征值与特征向量

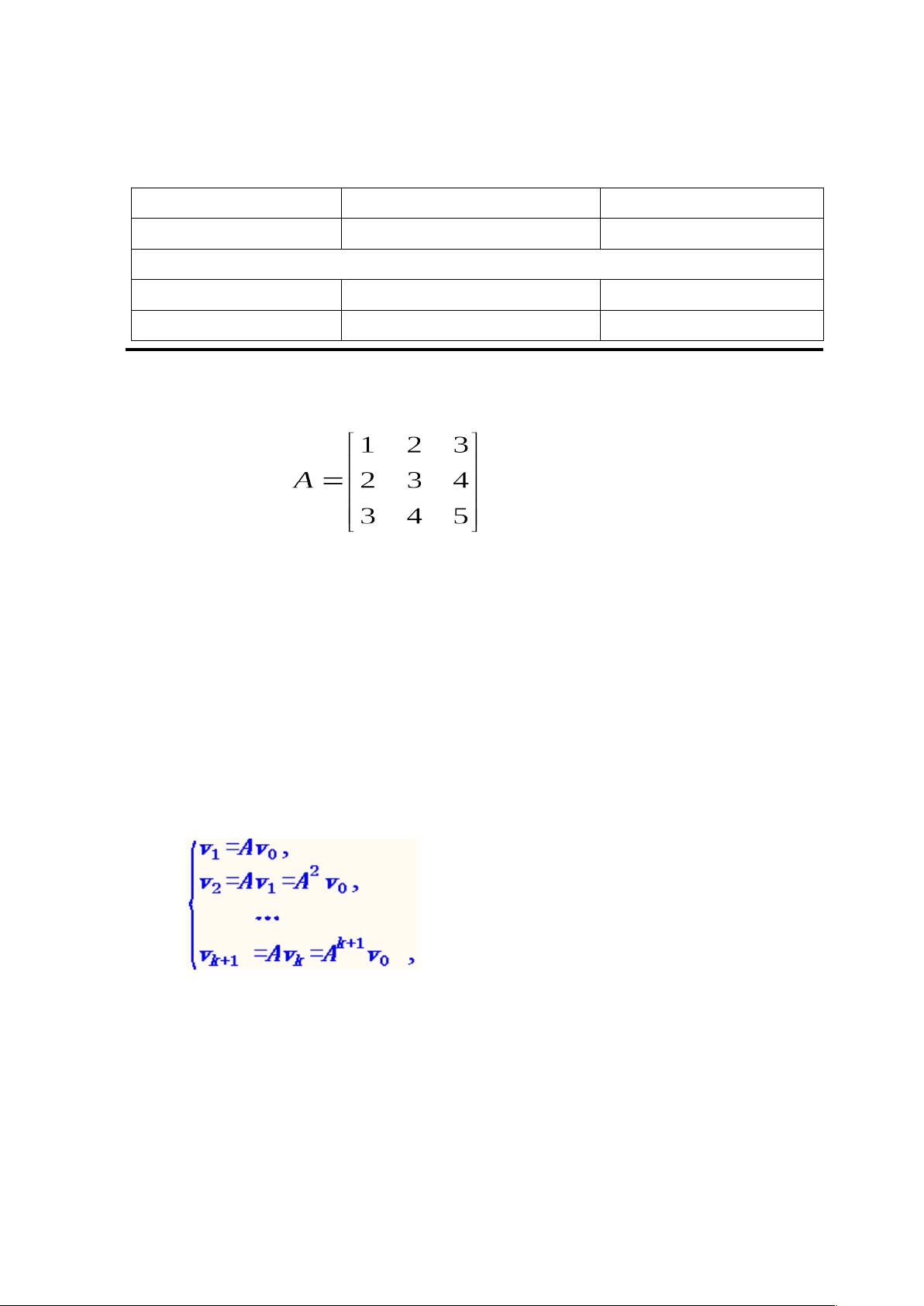
"矩阵特征值与特征向量的计算" 矩阵特征值与特征向量是线性代数中的核心概念，它们在许多领域如数据分析、控制理论、机器学习等都有着广泛的应用。特征值λ代表着矩阵作用于特定向量时的缩放因子，而特征向量则是该缩放操作下保持方向不变的向量。在本实验中，重点是使用幂法求解矩阵的主特征值及其对应的特征向量。 幂法是一种迭代求解方法，特别适用于求解大型稀疏矩阵的主特征值。其基本思路是选取一个非零初始向量ν0，并通过不断与矩阵A相乘来迭代更新向量，使得向量序列逐步接近特征向量。矩阵A的特征值λ1是最大的特征值（按绝对值），满足条件|λ1|>|λ2|≥|λ3|≥…≥|λn|，幂法会使得向量序列νk/λ1k随着迭代次数k的增加而趋近于λ1对应的特征向量x1。 在实验过程中，首先需要编程实现幂法的算法，选择合适的编程语言，如C语言。程序需要包含初始化向量、迭代计算、判断收敛等步骤。然后，通过计算机运行程序并输出计算结果，这通常包括特征值和特征向量的数值。关键代码可能涉及矩阵乘法、向量除法以及收敛性检查等操作。 在调试阶段，可能会遇到数值稳定性问题、程序逻辑错误或者收敛速度过慢等挑战。这些问题需要通过分析错误信息、优化算法或调整迭代次数来解决。实验总结部分，学生会分享他们在实验中遇到的具体问题、错误的原因分析，以及他们对幂法的理解和应用体会。 需要注意的是，幂法虽然简单易实现，但其收敛速度受到矩阵特征值分布的影响。如果矩阵有重叠的特征值或者特征值的模相差不大，幂法的收敛可能会变得缓慢。因此，在实际应用中，可能需要结合其他方法，如 QR 分解、雅可比方法或高斯-赛德尔迭代等，以提高计算效率。 在实验的最后，会给出程序源代码示例，这通常包括必要的头文件、常量定义、主函数以及计算特征值和特征向量的函数。例如，C语言的代码可能涉及到<stdio.h>和<math.h>库，使用定义的常量如MAX_N表示矩阵的最大维度，MAXREPT表示最大迭代次数，以及EPSILON表示收敛精度阈值。 这个实验旨在让学生深入理解矩阵特征值和特征向量的概念，掌握使用幂法求解特征值的技巧，同时培养他们的编程能力和问题解决能力。通过这样的实践，学生能够更好地将理论知识应用于实际问题中。