心理统计学：线性相关与散点图分析

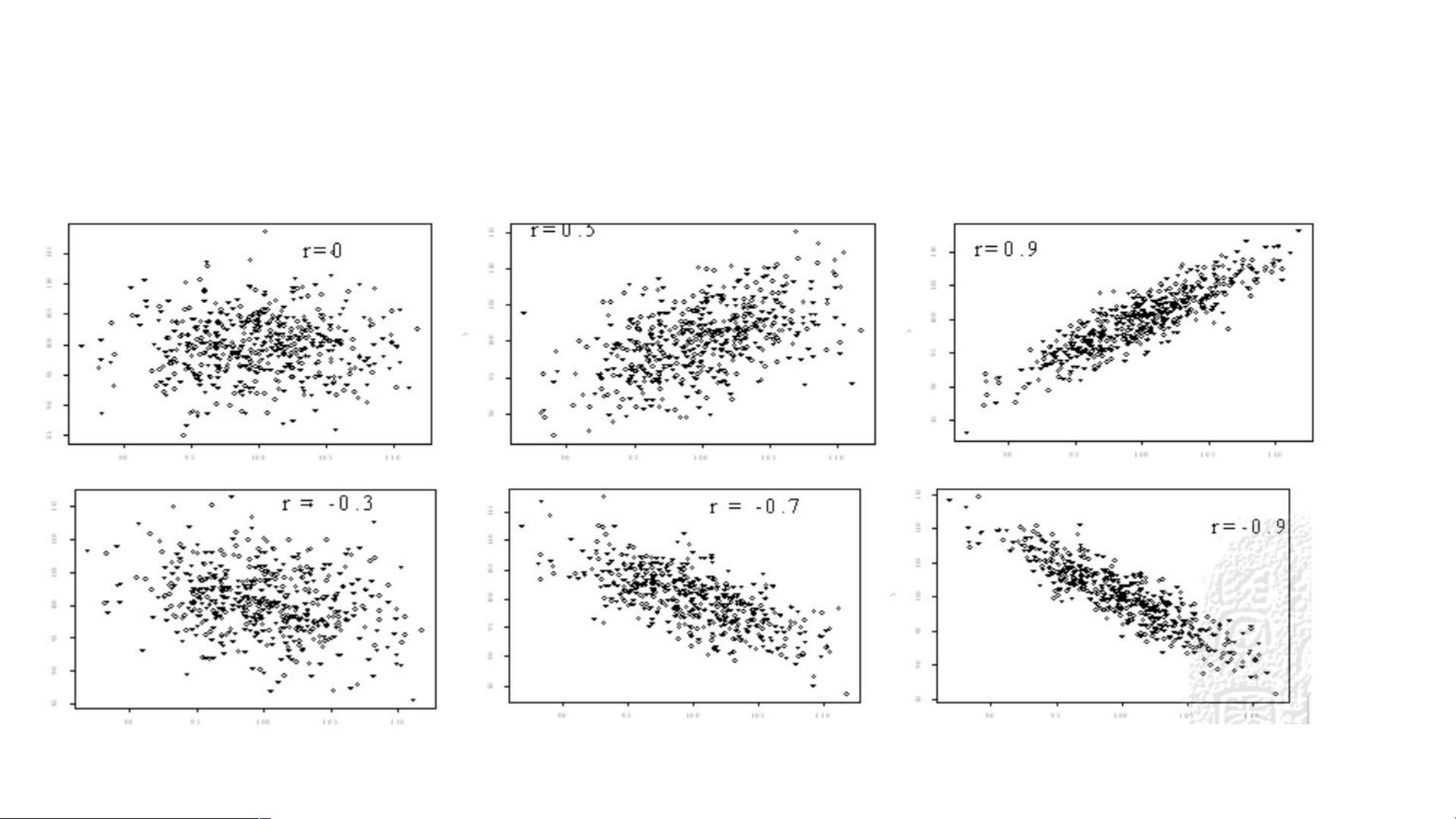
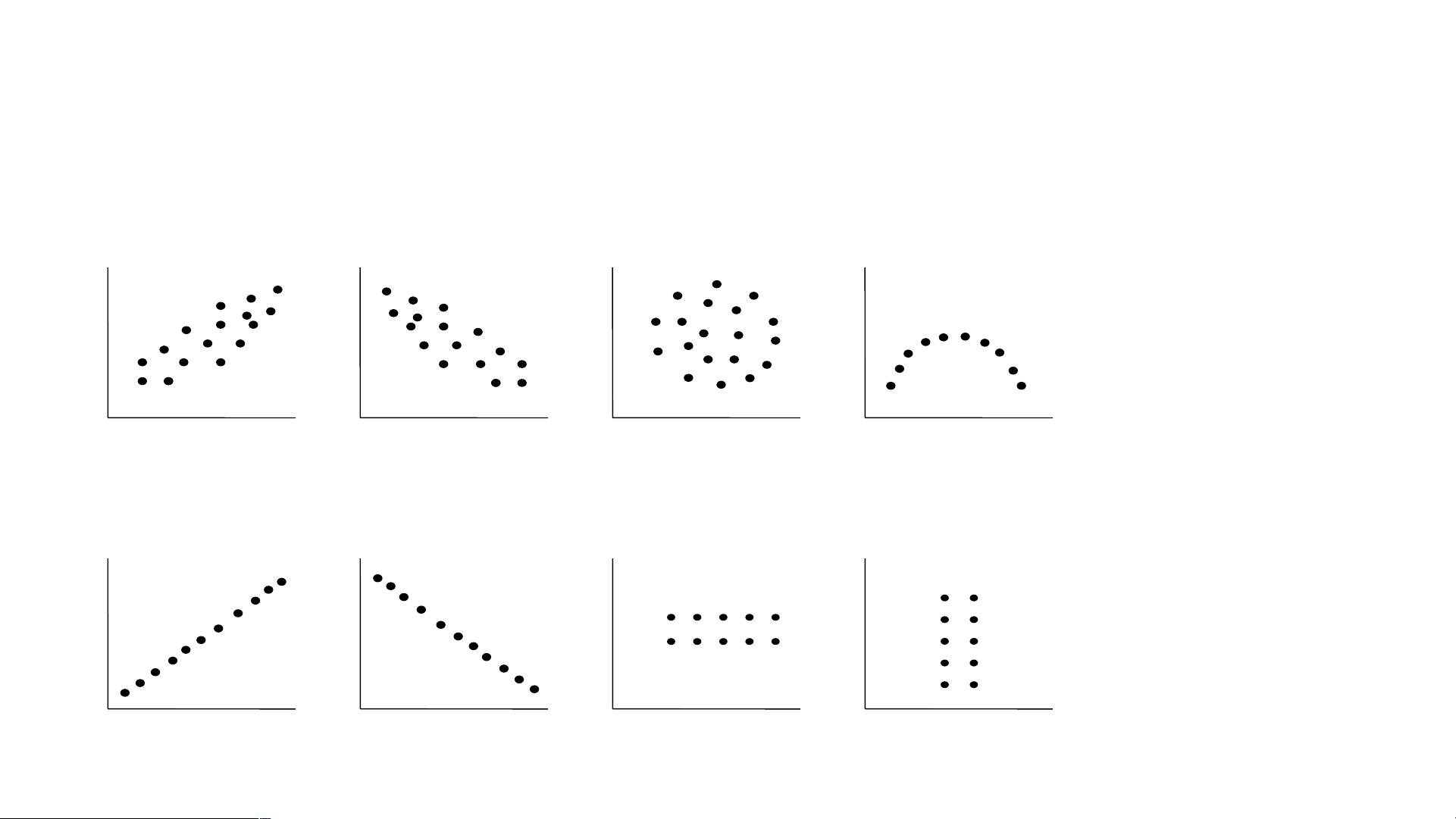
"第三十七节 线性相关.pptx 是一份关于心理统计学的课程资料，主要讲解了相关分析，特别是皮尔逊积差相关的概念和应用。内容涵盖了散点图的制作、相关性的本质、协方差的性质和公式、相关系数的解释和显著性检验，以及决定系数的理解。此外，还涉及了如何在SPSS软件中进行相关分析的操作。" 本资料深入探讨了统计学中的一个重要概念——线性相关，这是心理统计学研究中常见的分析方法。首先，学习目标包括掌握散点图的制作，通过散点图可以直观地观察两个变量之间的关系，识别离群值并判断其线性相关程度。散点图的形状可以揭示变量间的关系类型，如正相关、负相关或无明显关系。 其次，资料介绍了协方差的概念，它是衡量两个变量共同变化的程度。协方差的公式是离差乘积之和，为了得到无偏估计，通常除以样本数量减一（N-1）。协方差的性质和对比方差的公式也有所提及，帮助理解变量间的共变性和异变性。 积差相关，即皮尔逊相关系数r，是衡量两个变量之间线性相关强度和方向的指标。r的取值范围在-1到1之间，正值表示正相关，负值表示负相关，0表示无线性相关。r的计算涉及到协方差和各自变量的标准差，标准化公式将两个变量转换到相同的尺度上，使得相关系数具有可比性。 相关系数的显著性检验是判断两个变量间线性关系是否显著的关键步骤。通常采用Fisher的t检验，在小样本条件下，如果x和y均服从正态分布且总体相关系数ρ为0的假设下，通过计算t统计量并与临界值比较，做出拒绝或接受零假设的决策。这个过程包括提出零假设（ρ=0）和备择假设（ρ≠0），计算t值，查找t分布表确定显著性水平下的临界值，最后根据t值与临界值的比较做出结论。 此外，决定系数（R²）也被提及，它表示因变量变异中的比例是由自变量解释的，是相关系数平方的另一种表达形式，有助于评估模型的拟合优度。 这份资料提供了全面而详细的相关分析理论和实践指导，对于学习统计学、心理学，尤其是准备考研的学生来说，是一份宝贵的参考资料。通过学习这部分内容，学生可以熟练掌握如何分析和解释变量间的线性关系，以及如何在实际数据处理中运用这些统计方法。