of M’s step and direction of D’s step.
Algorithm 2 AdaGraft meta-optimizer
1: Input: Optimizers M, D; initializer w
1
; > 0.
2: Initialize M, D at w
1
.
3: for t = 1, . . . , T do
4: Receive stochastic gradient g
t
at w
t
.
5: Query steps from M and D:
w
M
:= M(w
t
, g
t
), w
D
:= D(w
t
, g
t
).
6: Update with grafted step:
w
t +1
← w
t
+
kw
M
– w
t
k
kw
D
– w
t
k +
· (w
D
– w
t
) .
7: end for
Layer-wise vs. global grafting.
Two natural variants of Algorithm 2 come to mind, especially if one is
concerned about efficient implementation (see Appendix C.1). In the layer-wise version, we view w
t
as a
single parameter group (usually a tensor-shaped variable specified by the architecture), and apply AdaGraft
and its child optimizers to each group. In the global version, w
t
contains all of the model’s weights. We
discuss and evaluate both variants, but our main experimental results use layer-wise grafting.
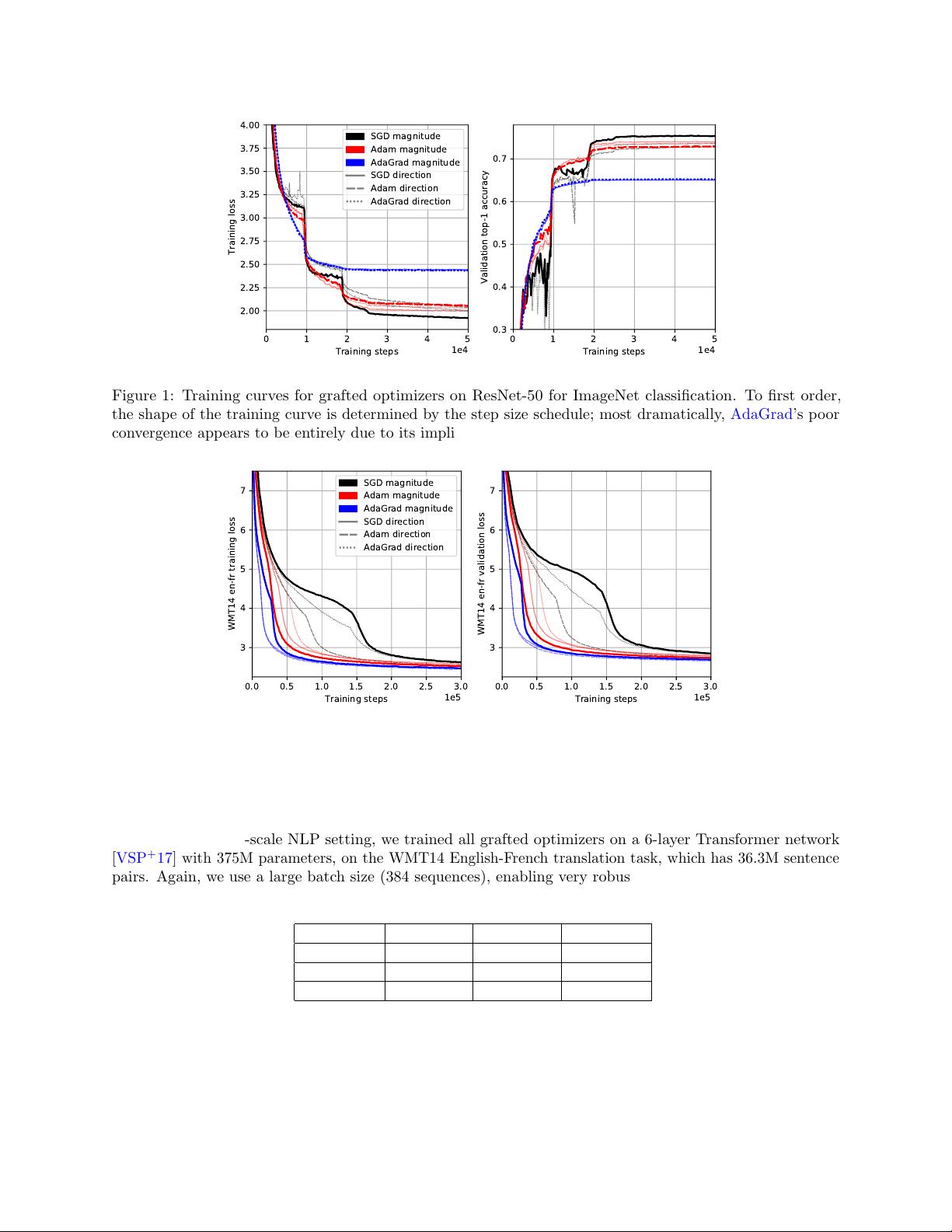
The first experimental question addressed by AdaGraft is the following: To what degree does an optimizer’s
implicit step size schedule determine its training curve? To this end, given a set of base optimizers, we can
perform training runs for all pairs (
M
,
D
), where grafting (
A
,
A
) is understood as simply running
A
. For the
main experiments, we use SGD, Adam, and AdaGrad, all with momentum β
1
= 0.9.
All experiments were carried out on 32 cores of a TPU-v3 Pod [
JYP
+
17
], using the Lingvo [
SNW
+
19
]
sequence-to-sequence framework built on top of TensorFlow [ABC
+
16].
3.2 ImageNet classification experiments
We ran all pairs of grafted optimizers on a 50-layer residual network [
HZRS16
] with 26M parameters, trained
on ImageNet classification [
DDS
+
09
]. We used a batch size of 4096, enabled by the large-scale training
infrastructure, and a learning rate schedule consisting of a linear warmup and stepwise exponential decay. All
details can be found in Appendix C.2.
Table 2 shows top-1 and top-5 accuracies at convergence. The final accuracies at convergence, as well as
training loss curves, are very stable (
<
0.1% deviation) across runs, due to the large batch size. Figure 1
shows at a glance our main empirical observation: that the shapes of the training curves are clustered by the
choice of M, the optimizer which supplies the step magnitude.
We stress that no additional hyperparameter tuning was done in these experiments; not even the global
scalar learning rate needed adjustment. Thus, starting with N tuned optimizer setups, grafting produces a
table of N
2
setups with no additional effort. Each row of this table controls for the implicit step size schedule.
M
D SGD Adam AdaGrad
SGD 75.4 · 92.6 72.8 · 91.2 73.7 · 91.4
Adam 74.1 · 91.9 73.0 · 91.3 73.7 · 91.6
AdaGrad 65.0 · 85.9 65.1 · 86.0 65.3 · 86.3
Table 2: Top-1 and top-5 accuracies at training step t = 50K for ImageNet experiments. Averaged over 3
trials; no accuracy varied by more than 0.1%.
5
剩余25页未读，继续阅读
syp_net
- 粉丝: 158
- 资源: 1187
我的内容管理
展开
最新资源
- AirKiss技术详解：无线传递信息与智能家居连接
- Hibernate主键生成策略详解
- 操作系统实验：位示图法管理磁盘空闲空间
- JSON详解：数据交换的主流格式
- Win7安装Ubuntu双系统详细指南
- FPGA内部结构与工作原理探索
- 信用评分模型解析：WOE、IV与ROC
- 使用LVS+Keepalived构建高可用负载均衡集群
- 微信小程序驱动餐饮与服装业创新转型：便捷管理与低成本优势
- 机器学习入门指南：从基础到进阶
- 解决Win7 IIS配置错误500.22与0x80070032
- SQL-DFS：优化HDFS小文件存储的解决方案
- Hadoop、Hbase、Spark环境部署与主机配置详解
- Kisso：加密会话Cookie实现的单点登录SSO
- OpenCV读取与拼接多幅图像教程
- QT实战：轻松生成与解析JSON数据
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
