汉诺塔问题C++递归解法详解

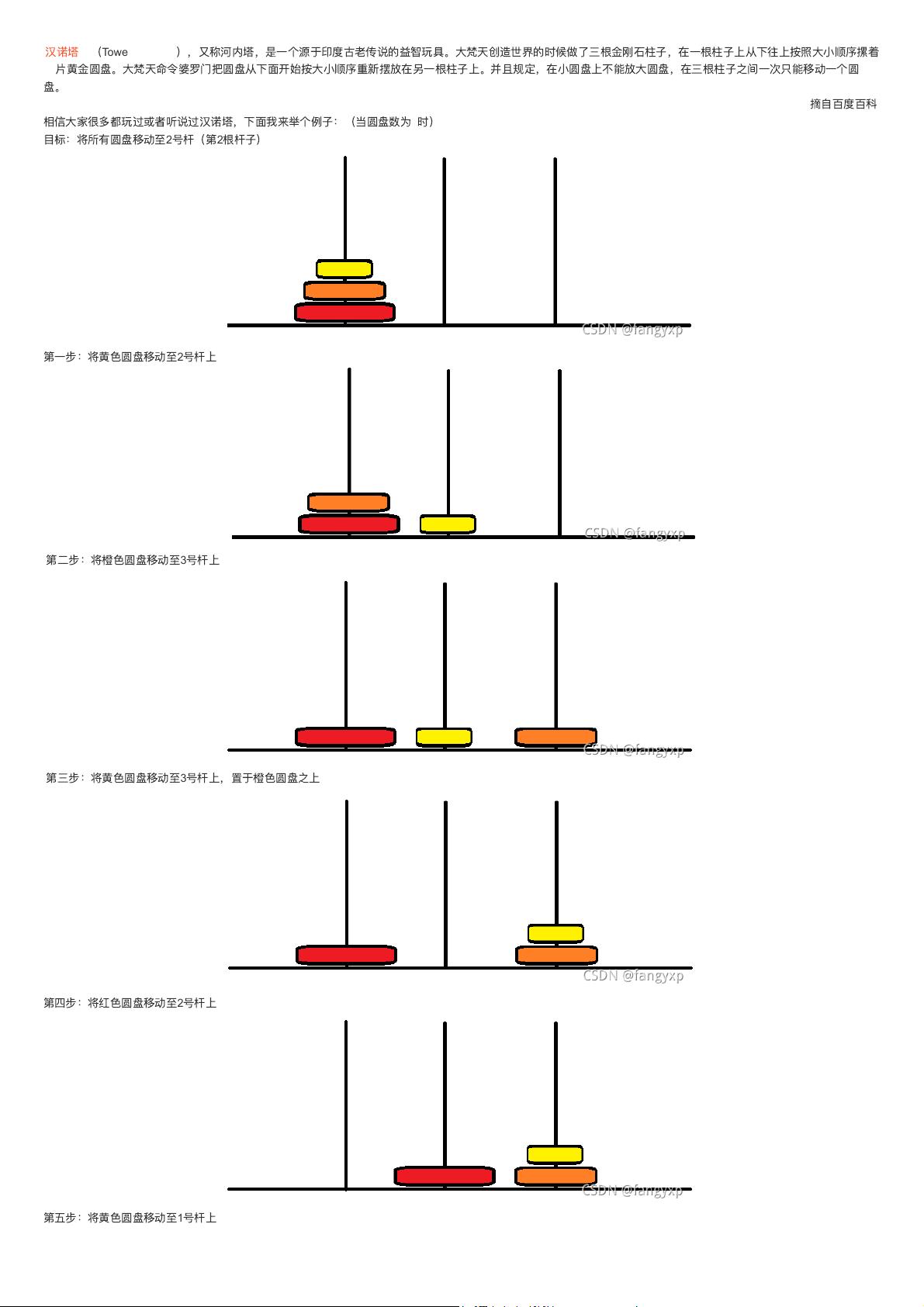
"汉诺塔问题c++递归详解" 汉诺塔问题是一个经典的计算机科学问题，源自古老的印度传说。它涉及到三根柱子和一系列大小不等的圆盘，目标是将所有圆盘从一根柱子（初始柱）按照大小顺序移动到另一根柱子（目标柱），同时遵循以下规则： 1. 每次只能移动一个圆盘。 2. 不允许将一个较大的圆盘放在较小的圆盘上方。 问题的核心在于递归策略的运用。递归是一种编程技术，通过函数或过程调用自身来解决问题。在这个问题中，我们可以将汉诺塔问题分解为三个子问题： 1. 将最上面的n-1个圆盘从初始柱移动到中间柱。 2. 将最大的圆盘从初始柱移动到目标柱。 3. 将中间柱上的n-1个圆盘移动到目标柱，这些圆盘原本在最大的圆盘下方。 当圆盘数量为n时，根据递归思想，我们可以得到以下步骤总数的公式： 步数 = 2^n - 1 例如，对于3个圆盘，总共需要7步；对于4个圆盘，需要15步；对于5个圆盘，需要31步，以此类推。 在C++中实现汉诺塔问题的递归解法，可以定义一个函数，该函数接受三个参数，分别代表起始柱、辅助柱和目标柱。基本的函数结构如下： ```cpp void hanoi(int n, char from_rod, char to_rod, char aux_rod) { if (n > 0) { // Step 1: Move n-1 disks from 'from_rod' to 'aux_rod' hanoi(n - 1, from_rod, aux_rod, to_rod); // Step 2: Move the nth disk directly from 'from_rod' to 'to_rod' cout << "Move disk " << n << " from rod " << from_rod << " to rod " << to_rod << endl; // Step 3: Move n-1 disks from 'aux_rod' to 'to_rod' hanoi(n - 1, aux_rod, to_rod, from_rod); } } ``` 在这个函数中，我们不断调用自身，每次处理更小规模的问题，直到只剩下一个圆盘，这时可以直接将其移动到目标柱。递归的本质使得程序能够解决任意规模的汉诺塔问题，而不需要显式地编写针对每种可能圆盘数量的代码。 汉诺塔问题展示了递归在解决复杂问题时的强大能力。理解递归不仅可以帮助解决类似汉诺塔的问题，而且在设计和实现许多其他算法（如树遍历、图搜索等）时也至关重要。通过递归，我们可以将复杂的问题分解为更简单的子问题，从而更容易理解和求解。在C++编程中，掌握递归是提升算法设计能力和解决问题的关键技能之一。