SAS假设检验基础：参数估计与置信区间

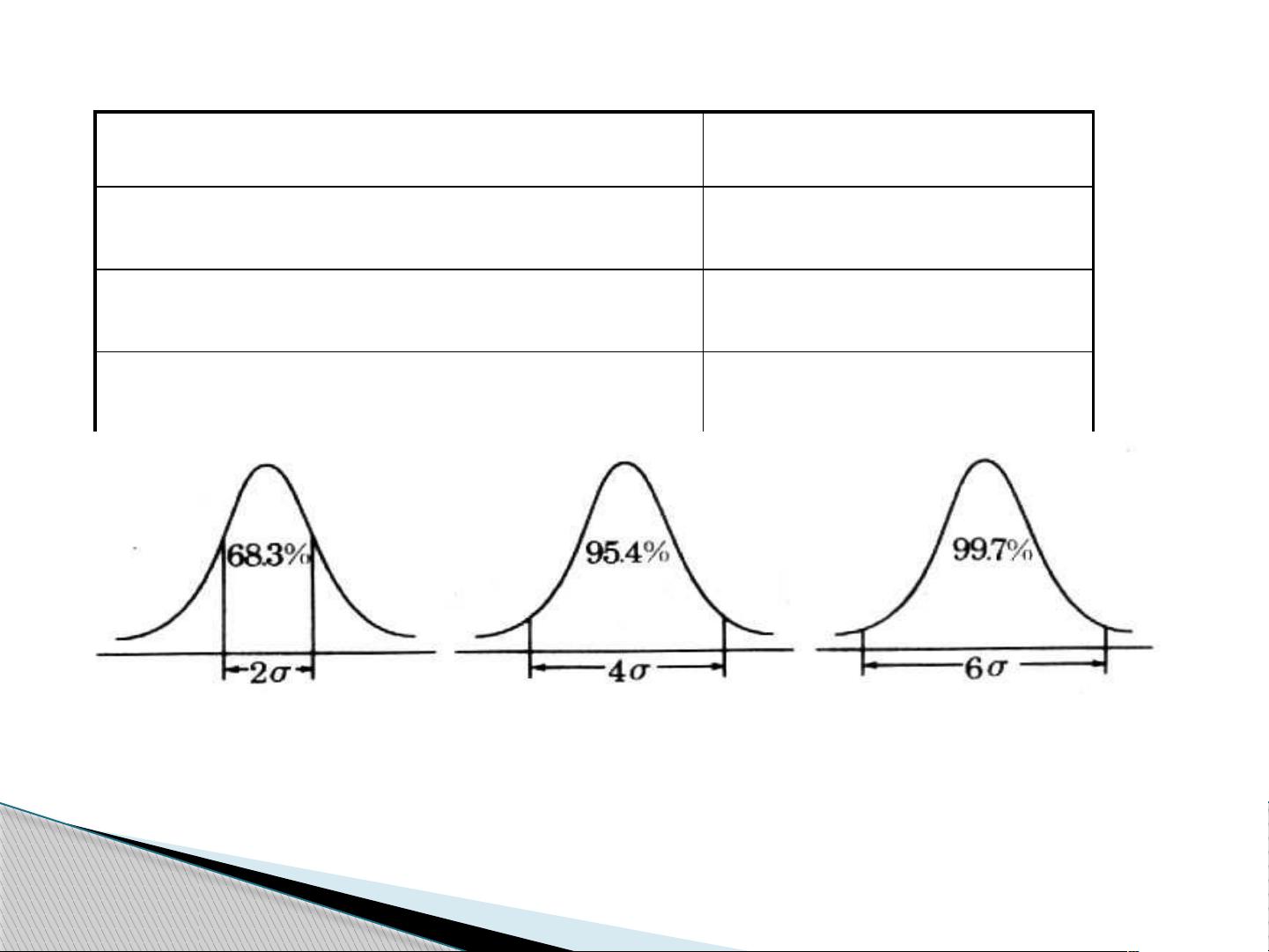
"SAS假设检验课程的PPT，主要涵盖了参数估计与假设检验的基本概念，包括点估计和区间估计的详细解释，以及置信区间的计算和正态分布的应用。" 在统计学中，假设检验是基于样本数据来判断关于总体参数的假设是否成立的一种方法。在SAS软件中，这一过程对于数据分析至关重要。本课件主要讲解了两个关键概念：参数估计和假设检验。 参数估计是统计推断的基础，分为点估计和区间估计。点估计是使用样本统计量（如样本均值、样本方差）直接对应到总体参数的估计值。而区间估计则更注重不确定性，它提供了一个范围，使得总体参数在这个范围内有特定概率（置信水平）被包含。置信区间是由样本统计量、抽样标准误差和置信水平共同确定的，比如95%的置信区间意味着我们有95%的把握认为总体参数在这个区间内。 在介绍点估计和区间估计时，课程提到了正态分布的重要性。正态分布，或高斯分布，是一种在很多自然现象中常见的连续分布，其特点是呈钟形曲线，对称且中间高两边低。在正态分布中，数据的分布特性可以用均值和标准差来描述，这在参数估计中非常有用。例如，68-95-99.7法则指出，对于正态分布，数据大约68%位于均值的一个标准差内，95%位于两个标准差内，而99.7%位于三个标准差内。 在SAS中进行假设检验时，我们可以利用这些统计特性来测试关于总体参数的假设，比如总体均值、比例或者方差是否等于某个特定值，或者比较两个总体的参数是否存在显著差异。这通常涉及到构建零假设和备择假设，然后通过统计检验（如t检验、Z检验、卡方检验等）来决定是否拒绝零假设。 通过SAS软件，用户可以轻松地进行假设检验，包括选择合适的统计检验方法、输入数据、设定显著性水平α（通常为0.05或0.01）以及解读输出结果。SAS会计算出p值，如果p值小于α，那么通常我们会拒绝零假设，认为观测到的差异并非由随机变异造成，而是反映了真实的总体差异。 SAS假设检验的课程旨在帮助学习者理解如何运用统计方法对数据进行深入分析，从而得出关于总体的有意义的结论。通过点估计和区间估计，我们可以对未知参数有一个定量的理解，而通过假设检验，我们可以验证我们的假设是否基于数据成立，这对科学研究和决策制定具有重大意义。