方差分析：P值解读与实际应用实例

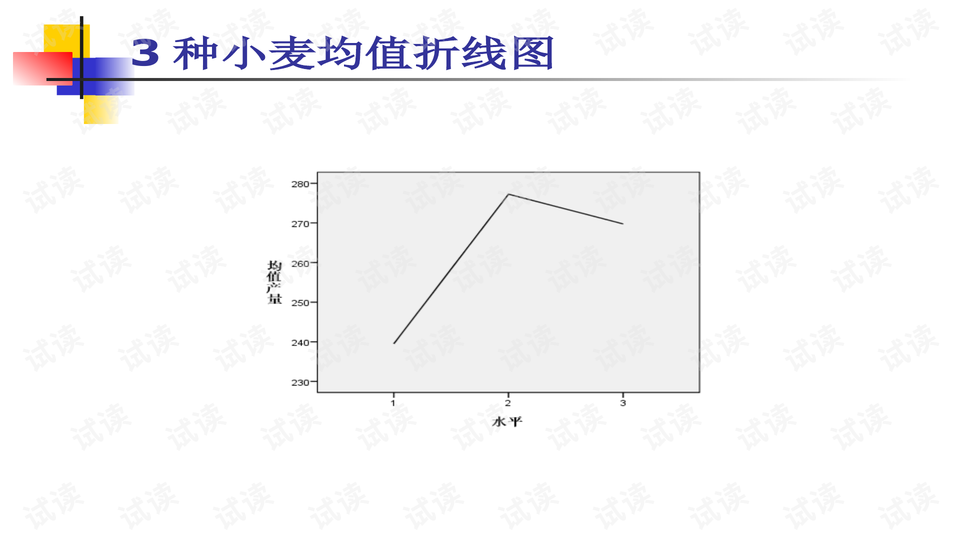
P值在R语言中的方差分析（Analysis of Variance, ANOVA）是一项统计方法，用于评估多个样本平均值之间是否存在显著差异。它起源于20世纪20年代的英国统计学家R.A.Fisher的工作，最初主要用于生物和农业的实验设计，后来被广泛应用于各个领域的数据分析。 在农业应用中，例如选择适合种植的小麦品种，通过比较不同品种在相同条件下种植的试验田产量，方差分析可以帮助确定哪种品种的产量有显著优势。比如，给出的数据中，通过计算各品种产量的均值和变异情况，我们能通过比较P值来判断产量之间的显著性差异。 在工业领域，如布料的缩水率测试，通过对比使用不同染整工艺处理后的布料，P值可以帮助检验染整工艺是否对缩水率产生了显著影响。在样本数据中，通过分析每个工艺对应的缩水率，我们可以通过方差分析来确定哪种工艺可能导致了显著的差异。 医学研究也常常利用方差分析，如探究细胞在不同溶液（如BMP4和BMP7）刺激下的变化。通过对细胞在不同时间点（24小时、48小时和72小时）的测量结果进行分析，可以检测出在特定溶液下，细胞响应是否具有显著的时空模式。 P值的大小至关重要，它代表了观察到的效应是否可能仅仅是由于随机误差造成的。如果P值小于预设的显著性水平（如0.05或0.01），通常认为观察到的差异是真实的，而不是偶然；反之，如果P值大于这个阈值，我们不能拒绝零假设，即各组间没有显著差异。在R语言中，我们可以使用诸如`anova()`函数进行方差分析，并根据输出的P值和其他统计量来解读结果。 总结来说，P值在R语言的方差分析中扮演着关键角色，它帮助研究人员判断不同组间的差异是否具有统计学意义，这对于科学决策和实验设计至关重要。通过结合实际案例，我们可以深入理解P值在不同场景下的具体应用和解读。