L型阵列二维方向估计：计算子空间新方法

192 浏览量更新于2024-08-30 收藏 908KB PDF 举报

"这篇研究论文主要探讨了一种针对L型阵列的二维方向估计的高效计算子空间方法，被收录在IEEE Transactions on Signal Processing期刊上，编号为T-SP-10768-2010。作者Shahram Shahbazpanahi向西安交通大学的Jingmin Xin教授发送了关于该论文的接受通知，要求进行必要的修订后发表。" 在信号处理领域，L型阵列因其独特的结构特性，被广泛用于二维方向估计。这种阵列由两个垂直和水平排列的天线组成，形成一个L形状，从而能够同时获取水平和垂直方向的信息，适用于多维度的空间信号源定位。论文的核心是提出了一种新的、计算效率高的子空间基础方法来改进二维方向估计的性能。传统的方法通常包括基于阵列信号处理的算法，如音乐（MUSIC）谱估计或埃瓦尔德（Ewald）对称配对法，这些方法虽然在一定程度上能实现二维方向估计，但计算复杂度较高，不适合实时或大规模的数据处理。论文中提出的计算子空间方法旨在解决这一问题，通过优化算法设计，降低了计算复杂度，同时保持了估计精度。具体来说，该方法可能涉及以下步骤： 1. **数据预处理**：首先，从接收到的信号中提取阵列数据，去除噪声和干扰，这通常包括去均值、滤波等操作。 2. **子空间分解**：利用奇异值分解（SVD）或者矩阵特征分解等技术，将阵列数据投影到低秩子空间，以便提取信号特征。 3. **特征向量选择**：根据L型阵列的几何特性，选择特定的特征向量，这些向量与目标信号源的方向角有关。 4. **构建二维谱估计**：在水平和垂直两个维度上分别构造谱函数，结合特征向量，形成一个二维的估计域。 5. **峰值检测**：通过寻找谱函数中的最大值，确定信号源的二维方向。 6. **优化与修正**：对初始估计进行迭代优化，可能采用梯度下降或最小二乘等方法，以提高估计精度。 7. **性能评估**：最后，通过仿真或实际数据验证方法的有效性，比较与其他方法的性能差异，例如误差性能、计算速度等。此方法的优势在于其在保证估计性能的同时，大大减少了计算量，这对于资源有限的系统或实时应用尤其重要。此外，这种方法可能还考虑了阵列不完美性（如相位误差、阵元位置偏差等）的影响，并提供了相应的补偿策略。这篇论文为L型阵列的二维方向估计提供了一个计算效率高、适应性强的新方案，对于信号处理领域的理论研究和实际应用都具有重要的参考价值。通过实施必要的修订，论文有望在IEEE Transactions on Signal Processing上正式发表，进一步推动相关领域的技术进步。

IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. XX, NO. YY, SEPTEMBER 2010 2

response vector of two overlapping subarrays of each ULA,

a modiﬁed propagator method (MPM) with eigendecompo-

sition was presented to estimate the elevation and azimuth

angles independently from the covariance matrix of combined

received data of two overlapping subarrays of each ULA [3].

However unlike the ordinary propagator method (PM) [9], the

least-square (LS) estimation of the linear propagator is seri-

ously affected by the non-zero correlations of additive noises

between two overlapping subarrays, and correspondingly the

angle estimates are biased regardless of the signal-to-noise

ratio (SNR). Furthermore a pair-matching procedure is still

required to associate the elevation and azimuth estimates due

to the independent orderings of the array response vectors of

two ULAs in terms of the elevation or azimuth angles and that

of eigenvalues of two above-mentioned covariance matrices

for 1-D DOA estimation with respect to each ULA [4], [8].

By dividing one ULA into two overlapping subarrays to gain

the shift invariance of these subarrays, a joint singular value

decomposition (SVD) based method (JSVD) was suggested

to 2-D DOA estimation with automatic pairing by using

two cross-correlation matrices (CCMs) between two subarrays

and another ULA [5], where the effect of additive noise is

mitigated. The key point of [5] and its variants [35], [36] is the

ordering exchange of a product of the source signal covariance

matrix and a diagonal matrix of the phase delays with respect

to the elevation or azimuth angle, which is only valid when

the the source signal covariance matrix is diagonal matrix.

Unfortunately the JSVD [5] performs worse in the estimation

of azimuth angle even in the case of uncorrelated signals

when the number of snapshots is small, because the nonzero

cross-correlations in the estimated source signal covariance

matrix couple up the array response vectors in terms of the

azimuth angle, and it results in inaccurate parameter estimate

even at high SNR. An alternative cross-correlation matrix and

SVD based method was proposed for 2-D DOA estimation

with automatic pairing [7], but it involves the minimization

of a constrained nonlinear function and necessitates a prior

knowledge of the powers of incident signals. By a introducing

an auxiliary electric angle as a function of the elevation and

azimuth angles and adopting the 1-D generalized ESPRIT

method [34], a joint estimation method was proposed with-

out pair-matching procedure [31], however it requires two

computationally intensive eigenvalue decomposition (EVD)

processes and a restriction on the elevation and azimuth angles.

In addition, an elaborative CCM based pair-matching method

was developed [4], but it is seriously affected by the estimation

of the “virtual angles” of incident signals even though the

elevation and azimuth angles are estimated well [5].

Therefore the purpose of this paper is to investigate the

2-D DOA estimation of noncoherent narrowband signals

with the L-shaped array placed in the 𝑥–𝑧 plane in a new

computationally efﬁcient way. Since the eigendecomposition

(EVD or SVD) process is computationally intensive and

time-consuming [37], some computationally simple subspace-

based 1-D DOA estimation methods were proposed without

eigendecomposition (see [10] and references therein). In order

to eliminate the effect of additive noise and to reduce the com-

putational burden involved by the eigendecomposition, we pro-

( )

s n

−

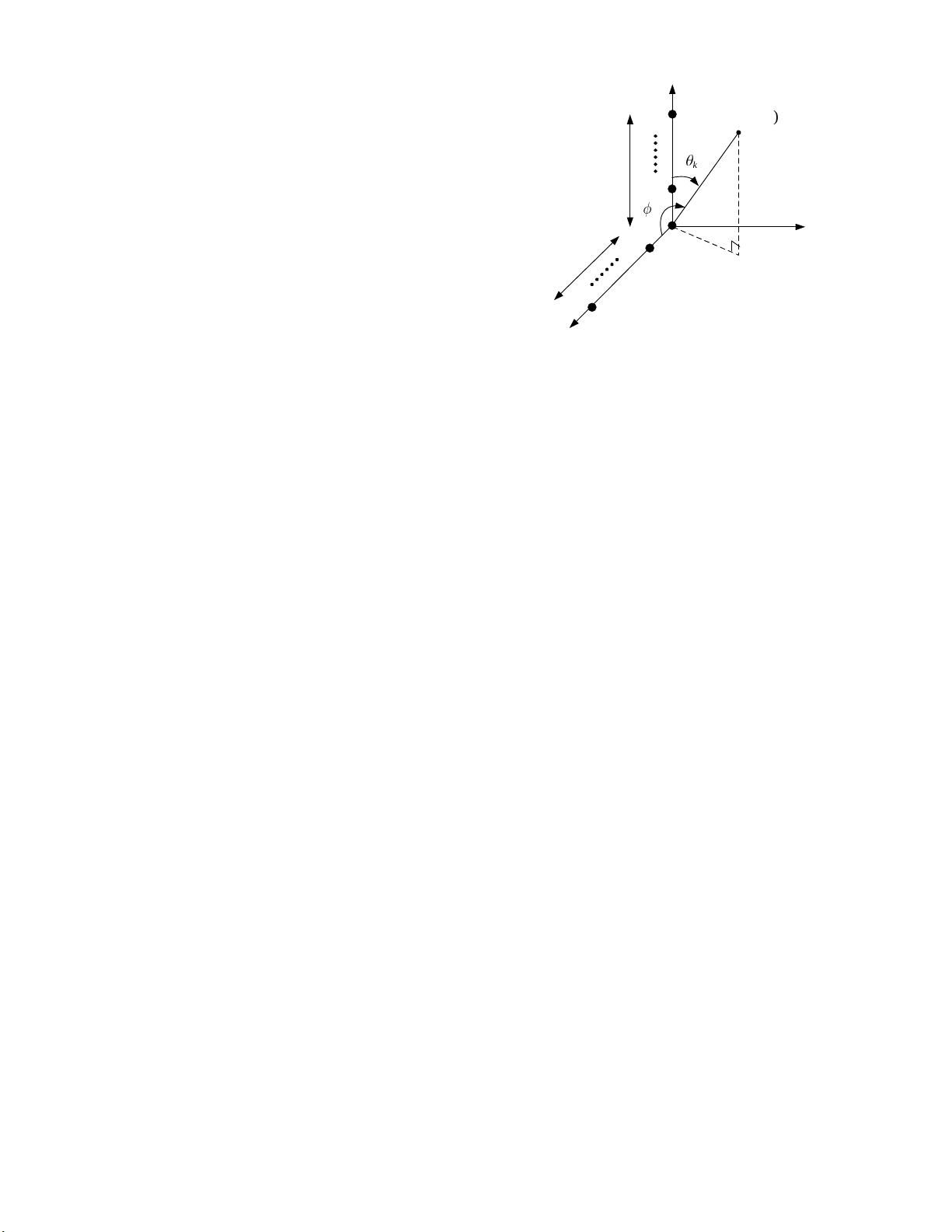
Fig. 1. The geometrical conﬁguration of the L-shaped array [4].

posed a subspace-based method without eigendecomposition

(SUMWE) for 1-D DOA estimation with the ULA [10], where

the full ULA is divided into overlapping forward and backward

subarrays, and the null space is obtained through a linear

operation of the combined Hankel correlation matrix,which

is formed from the cross-correlations of some senor data by

exploiting the shift invariance of ULA. Inspired the SUMWE,

we propose a new computationally efﬁcient cross-correlation

based 2-D DOA estimation (CODE) method without eigen-

decomposition by exploiting the array geometry of L-shaped

array. Firstly the elevation and azimuth angles are estimated

independently by a 1-D subspace-based estimation technique,

where the null spaces are obtained through a linear operation

of the matrices formed from the cross-correlation matrices

between the array data received by two ULAs, and then the

pair-matching can be conducted by searching the minimums of

a cost function of the azimuth and elevation angles, where the

eigencomposition is avoided in the both procedures. Moreover

the statistical analysis of the proposed DOA estimation method

is studied, and the explicit expressions of the asymptotic mean-

square-errors (MSEs) of the elevation and azimuth estimates

are derived. The effectiveness of proposed method and the the-

oretical analysis are substantiated through numerical examples.

The simulation results show that the proposed CODE method

has good estimation with a small number of snapshots and at

low SNR and there is good agreement between the theoretical

analyzes and empirical results.

II. DATA MODEL AND ASSUMPTIONS

As shown in Fig. 1, we consider the L-shaped array consist-

ing of two ULAs in the 𝑥-𝑧 plane, where each ULA has 𝑀

omnidirectional sensors with spacing 𝑑 and the sensor at the

origin of coordinates 𝑧

is the reference one for each ULA,

and suppose that 𝑝 noncoherent narrowband signals {𝑠

𝑘

(𝑛)}

with the wavelength 𝜆 are in the far-ﬁeld and imping on the

array from distinct directions with the elevation and azimuth

angles {𝜃

𝑘

, 𝜙

𝑘

}. Then the received signals at the ULAs along

the 𝑧 and 𝑥 axes are given by

𝒛(𝑛) = 𝑨(𝜃)𝒔(𝑛) + 𝒘

𝑧

(𝑛) (1)

𝒙(𝑛) = 𝑨(𝜙)𝒔(𝑛) + 𝒘

𝑥

(𝑛) (2)

剩余10页未读，继续阅读

weixin_38714370

粉丝: 3
资源: 905

L型阵列二维方向估计：计算子空间新方法

5_2_L型阵列二维ESPRIT算法的DOA估计.zip

基于增广矩阵束的L型阵列的二维DOA估计MATLAB程序_基于增广矩阵束的L型阵列的DOA估计_增广矩阵_矩阵束_

基于稀疏阵列的L型阵列波达方向估计.rar

l型阵列的二维doa估计仿真图matlab

在阵列信号处理中，如何利用L型阵列进行二维DOA估计？并探讨在该场景下MUSIC算法与ESPRIT算法的性能对比。

如何利用L型阵列实现二维DOA估计，并比较使用MUSIC算法和ESPRIT算法在该场景下的性能？

在L型阵列配置下，如何通过仿真比较MUSIC算法与ESPRIT算法在二维DOA估计中的性能差异？

matlab二维doa估计,阵列信号处理,一维、二维doa估计

二维music算法二维doa估计matlab程序

基于Matlab的子空间类算法在相干信号波达方向估计中的代码

最新资源