基于量化索引序列分析的G.723.1信道QIM隐藏攻击检测方法

170 浏览量更新于2024-08-27 收藏 789KB PDF 举报

本文主要探讨了在G.723.1语音编码流中检测量化指数调制(QIM)隐藏技术的新型方法。G.723.1是一种广泛用于VoIP（Voice over Internet Protocol）的压缩标准，其通过将连续信号转化为离散的量化指数序列来减小数据传输量。作者注意到，量化指数分布具有不平衡性和相关性这一关键特征，这是由于QIM隐藏信息时对原始编码进行微妙修改的结果。在QIM中，秘密信息通常被嵌入到音频信号的量化步骤中，通过对特定的量化索引（codeword）进行选择或改变。这些索引的选择会遵循某种模式，从而形成可以被用来隐藏信息的统计特性。论文提出了一种统计模型的设计，旨在提取这些不平衡性和相关性的量化索引分布特征，将其转换为定量特征向量。这些特征向量捕捉到了QIM隐藏操作的独特印记，有助于区分含有隐藏信息的编码流与正常编码流。为了构建一个有效的检测器，作者利用支持向量机(SVM)作为分类器。SVM是一种强大的机器学习算法，它能够处理高维数据并找到最优的决策边界，从而有效地识别出QIM隐藏的模式。通过训练集的学习和验证，这个模型能够准确地区分被QIM加密的G.723.1编码与未加密的编码，提高了检测的灵敏度和准确性。实验结果显示，该方法在实际应用中表现出了较高的检测性能，能够在不明显影响语音质量的情况下，有效地发现并定位嵌入在G.723.1编码中的QIM隐藏信息。这对于保护音频数据的隐私和安全具有重要意义，同时也展示了在数字信号处理领域中，针对特定编码标准的隐写术分析方法的研究进展。总结来说，这篇文章提供了一种基于量化索引序列分析的QIM隐藏检测策略，它利用统计模型和机器学习技术来识别G.723.1编码中的潜在隐藏信息，对于保证数字通信系统的安全性具有实用价值。

Li et al. / J Zhejiang Univ-Sci C (Comput & Electron) 2012 13(8):624-634

626

The QIM steganography hides the secret data

during the VQ process. If one codeword is selected

then one secret bit can be embedded. Taking the

embedded process based on L

as an example, the

CNV-QIM steganography (Xiao et al., 2008) firstly

partitions L

into two sub-codebooks

L and

using the CNV algorithm, where

L and

L both

contain |L

|/2 vector indices and satisfy

12 12

11 11 1

,.LL LLL  (2)

The CNV algorithm can guarantee that each

codeword and its most nearest codeword in L

belong

to different sub-codebooks. Thus, the additional sig-

nal distortion caused by QIM embedding would be

minimal in comparison with other division methods.

Upon the completion of partition, labels of ‘0’ and ‘1’

will be assigned to

and

, respectively. When a

secret bit is embedded, only the corresponding

sub-codebook is used for codeword selecting. On the

decoding side, the hidden bit is extracted through

checking which sub-codebook the codeword belongs to.

According to the above analysis, there are three

split vector sequences in the encoded speech bit

stream containing N G.723.1 frames. Each split vector

sequence F

can be represented as follows:

,1 , ,

, ..., , ...., , 1, 2, 3,

ii ik iN

iFf f f (3)

where f

i,k

(i{1, 2, 3}, k[1, N]) represents the ith

split vector of frame k in the bit stream. After VQ, F

will be converted to quantization index sequence

(QIS) S

,1 , ,

,..., ,...., , 1, 2, 3,

hu m

ii ik iN

Sc c c i (4)

where

( {1, 2, 3}, [1, ], [1, | |])

ik i

ci k Nu L

is the

quantization index of f

i,k

The QIM steganography (Xiao et al., 2008)

embeds the secret bits into the bit stream when f

i,k

chooses the quantization index. As a result of each

frame containing three split vectors, three secret bits

can be hidden in each frame. Obviously, the QIM

steganography will inevitably change the original

quantization result, because the QIM steganography

is able to convert the original quantization index

of f

i,k

into

().

cuh



Therefore, the original QIS S

of F

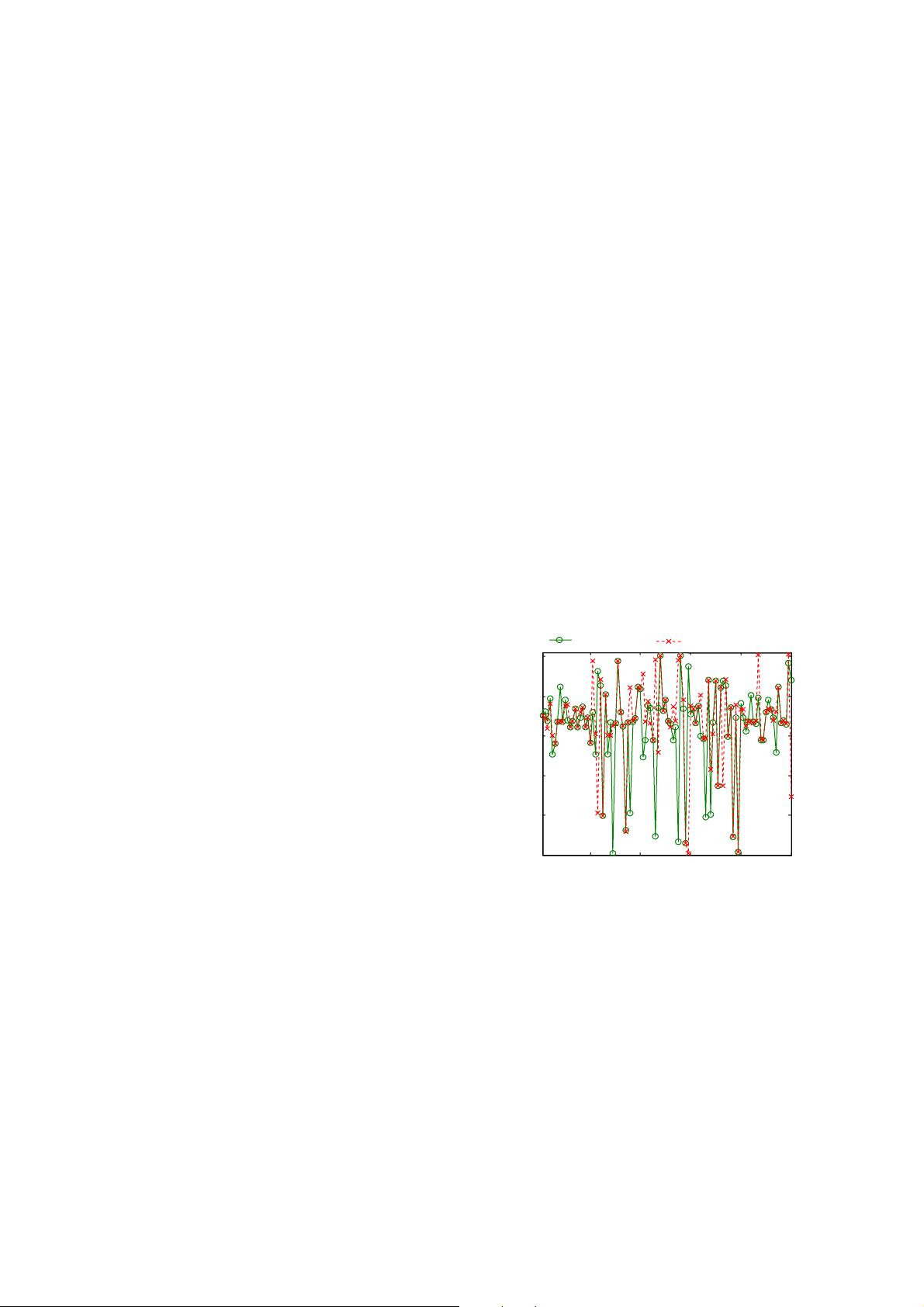
will produce disturbance. Fig. 1 presents an

example of the QIS disturbance. In this example, we

firstly encode a speech segment with a duration of 3 s

according to G.723.1 and obtain the ‘cover’ object.

Secondly, we repeat the encoding process to obtain

the ‘stego’ object using the QIM steganography (Xiao

et al., 2008). We extract the QIS

11,1 1,50

, ..., , ...,

Sc c

1,100

c from the encoded bit stream of the ‘cover’ and

‘stego’ objects. We show these two QIS in Fig. 1, and

we can clearly view the difference between the origi-

nal QIS and its steganography version; the QIM

steganography significantly changes the quantization

vector sequence. This disturbance of QIS is probable

to change the distribution characteristics of the quan-

tization index as well. Obviously, if these character-

istics can be quantified then the disturbance in QIS

can be measured. Taking advantage of this informa-

tion, we can detect QIM steganography in G.723.1 bit

stream.

3 Statistical models of quantization index

distribution characteristics

According to acoustics of speech production,

phoneme is the basic unit of human speech and is the

pronunciation of one or several sequential letters

(Thomas, 2002). When a person speaks, he/she con-

tinuously adjusts his/her articulators for a sequence of

Fig. 1 Example of quantization index modulation (QIM)

steganography disturbing the quantization index se-

quence (QIS) of the first split vector

20 40 60 80 100

100

150

200

250

Sequence number

Quantization index

Stego

Cover

剩余10页未读，继续阅读

weixin_38650842

粉丝: 4
资源: 977

基于量化索引序列分析的G.723.1信道QIM隐藏攻击检测方法

行业分类-设备装置-基于量化索引调制QIM的G.723.1语音信息隐写分析方法.zip

G.711 G.721 G.723声音压缩标准压缩、解压代码

An optimal adaptive quantization index modulation watermarking algorithm

Difference angle quantization index modulation scheme for image watermarking

AdaBits Neural Network Quantization With Adaptive Bit-Widths.pdf

Adaptive Loss-Aware Quantization for Multi-Bit Networks.pdf

quantization-Compressive-sensing.rar_1 bit quantization_1 bit 压缩

论文研究-Computerized Feature Quantization of Sublingual Vein Based on Color Information.pdf

Least Squares Quantization in PCM.pdf

H.264/SVC parameter optimization based on quantization parameter, MGS fragmentation, and user bandwidth distribution

最新资源