Matlab PDE Toolbox：解决三种偏微分方程的综合实验

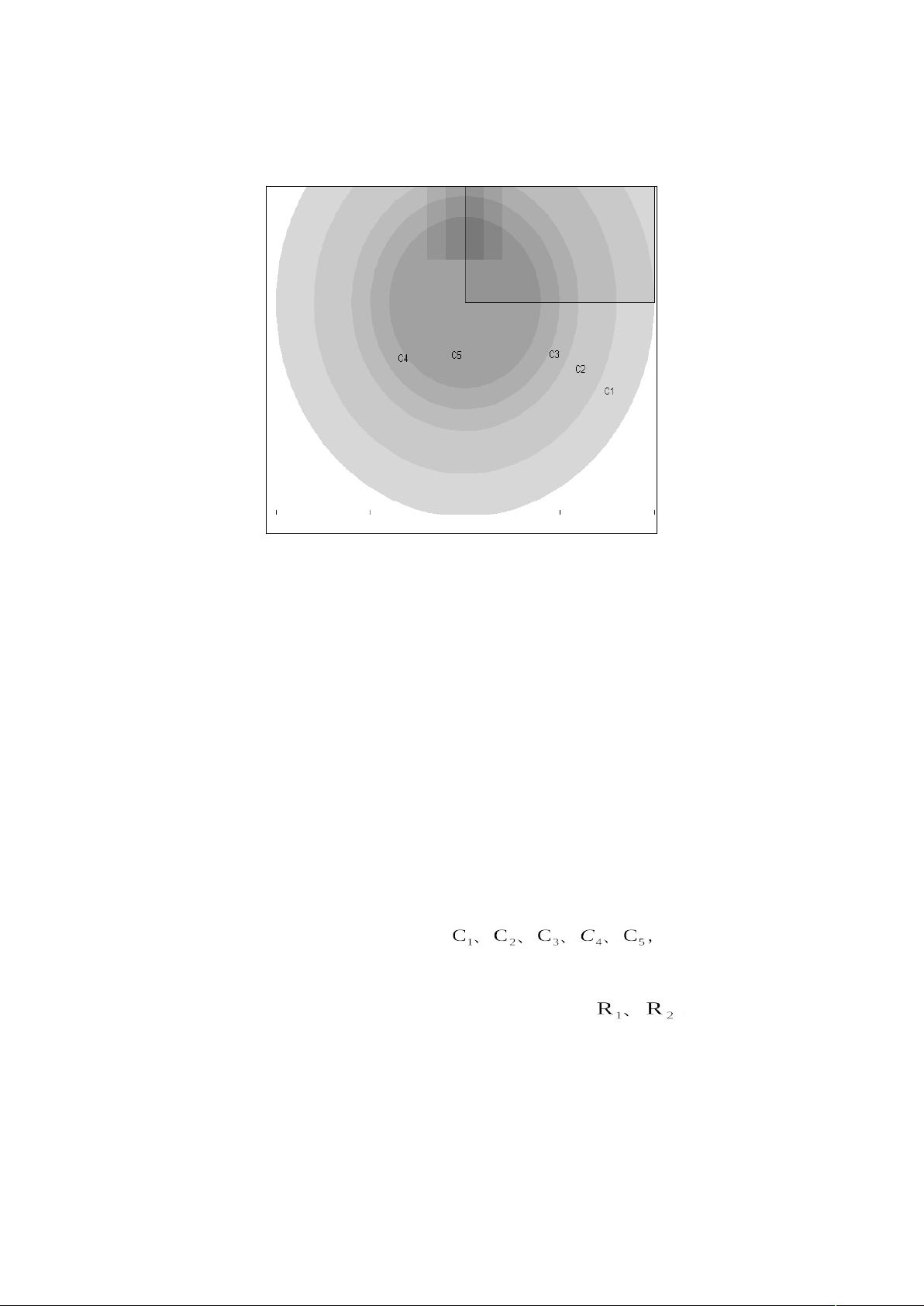
本实验旨在让学生深入理解和应用Matlab的PDE Toolbox来解决实际工程背景下的偏微分方程。实验要求2011届信计专业学生通过实践操作，掌握处理三种类型的偏微分方程——抛物型、椭圆形和双曲型的方法。实验内容包括以下几个关键步骤： 1. **抛物型方程**：首先，学生需要了解抛物型方程的一般形式，例如考虑一个具有物理意义的问题，如波动方程，用来描述振动或热传导。实验中，可能会涉及到扩散方程或波动方程的实例，这些方程可以通过PDE Toolbox中的函数如`assempde`来构建和求解。 2. **椭圆形方程**：具体到椭圆形方程，比如Helmholtz方程的变种，涉及一个圆形金属片中心挖去正方形区域的问题。外边界采用Neumann边界条件，内边界则采用Dirichlet条件。学生需要利用PDE Toolbox创建合适的几何区域（`scatterg`）和边界条件（`scatterb`），设置系数（如`c`, `a`, `f`），然后使用`initmesh`、`refinemesh`等函数进行网格初始化和细化，最终通过`assempde`求解并可视化结果。 3. **二维动画与代码实现**：实验中提供了二维动画的Matlab程序示例，展示了如何使用`echoon`和`clc`等命令控制程序流程，以及如何在复平面中求解。学生需要理解并调整这段代码，以适应不同类型的方程和边界条件，生成动态的解的三维图形和二维动画。 4. **实验报告与提交要求**：学生需按照提供的开题报告格式，清晰地陈述问题背景、方程描述、选择的解决方案、以及实验过程中遇到的问题和解决方案。整个过程不仅考验了学生的编程技能，还要求他们具备理论联系实际的能力，将偏微分方程的知识应用于实际工程问题。 通过这个实验，学生能够加深对Matlab PDE Toolbox的理解，提高解决实际工程问题的能力，并提升团队合作和报告撰写技巧。