西安交大非正弦周期电路详解与傅里叶级数应用

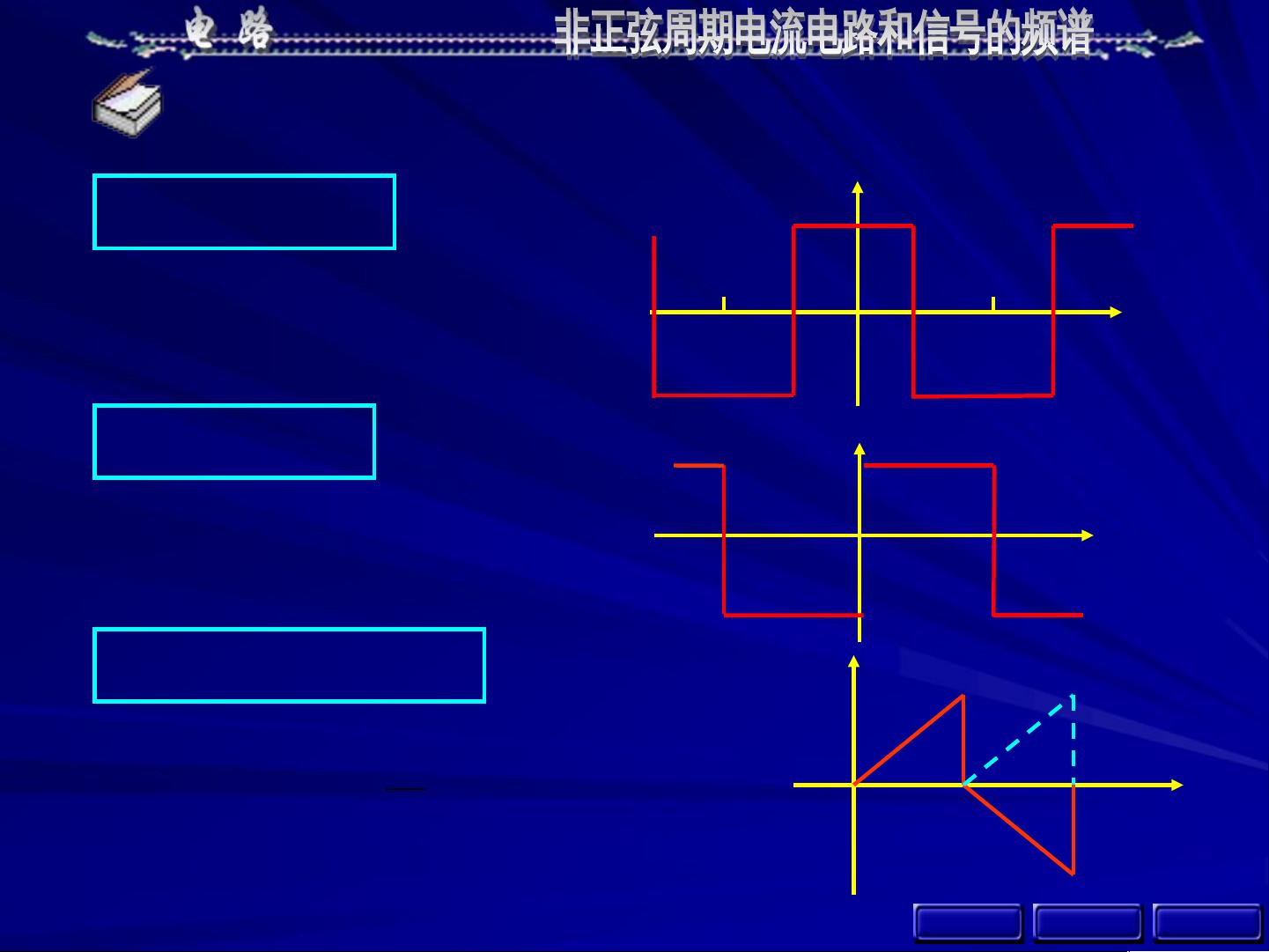
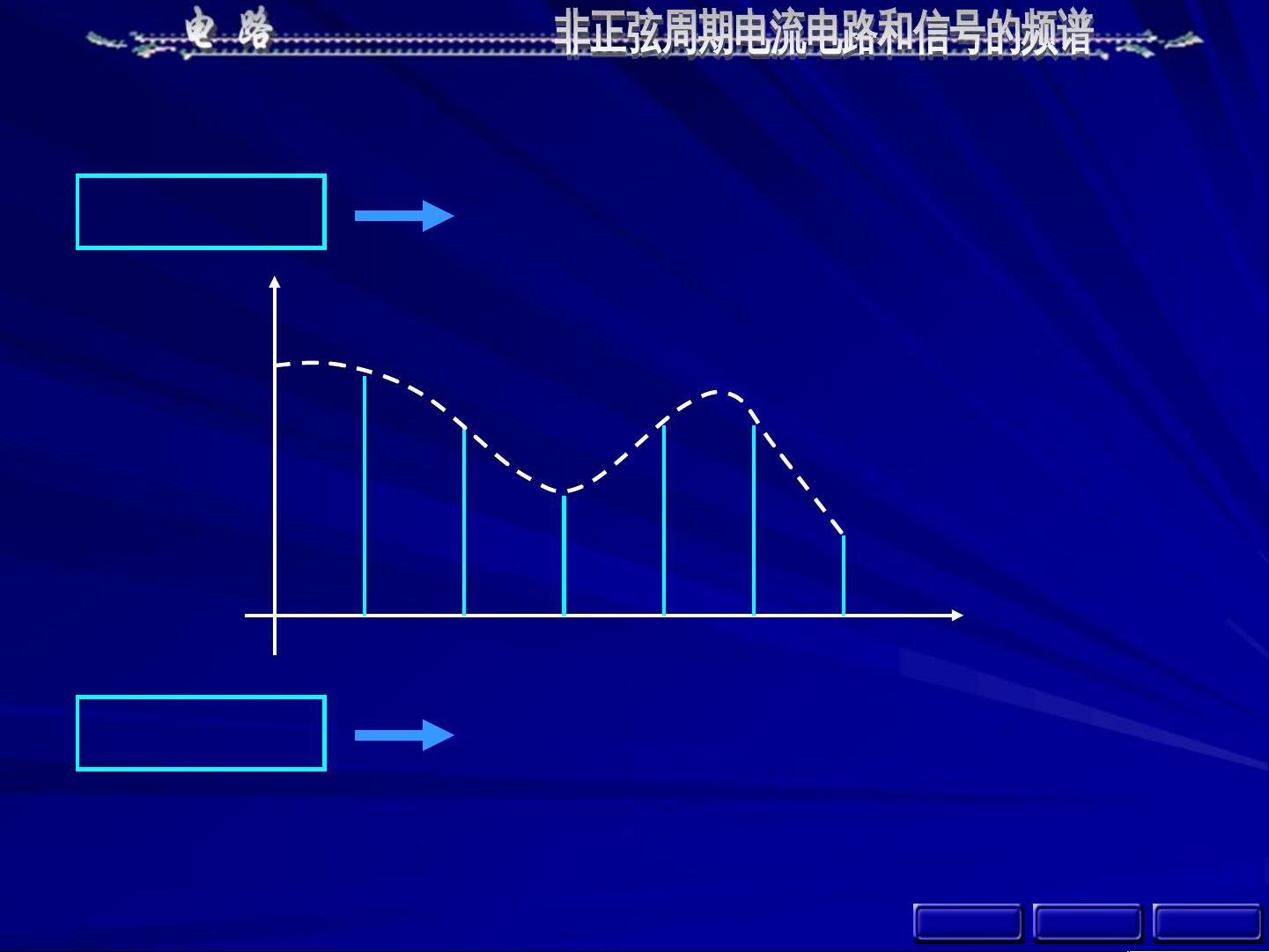
西安交通大学的电路分析课件深入探讨了非正弦周期电流电路的相关理论和应用，对于自学者而言具有很高的价值。课程的核心内容涵盖了以下几个关键部分： 1. **非正弦周期信号**：在实际工程中，如电子技术、自动化控制、计算机和无线电技术等领域，常常会遇到非正弦波形的电压和电流。这类信号的特点是非正弦波，但仍然遵循周期性变化。例如，锯齿波和半波整流电路的输出信号是非正弦周期信号。 2. **傅里叶级数分解**：这是处理非正弦周期函数的重要工具。非正弦周期函数如果满足狄里赫利条件（有限个极值点、间断点和一个周期内绝对可积），可以被展开为傅里叶级数。傅里叶级数包括直流分量（基波）、二次谐波（两倍频率）以及更高次谐波。这些谐波反映了信号的频率成分。 - **直流分量**：信号的基础频率成分，与原函数频率相同。 - **二次谐波**：频率是基础频率的两倍的信号成分。 - **高次谐波**：频率为基频的整数倍的信号，比如三次谐波、四次谐波等。 3. **有效值和平均功率**：对非正弦周期电流电路的计算，不仅涉及信号的瞬时值，还包括有效值（衡量其长期平均效应）和平均功率（能量传输的度量），这些都是理解和设计电路性能的关键。 4. **对称三相电路中的高次谐波**：在电力系统中，特别是三相交流电路，高次谐波的分析尤为重要，因为它们可能引起电网的不稳定和设备损耗。 5. **傅里叶级数的指数形式和积分简介**：这部分介绍了傅里叶级数的另一种表达方式，并可能引入傅里叶积分的概念，以便更深入地理解信号的频域特性。 6. **实例分析**：通过具体的例子，如示波器内的水平扫描电压和半波整流电路输出，让学生能够将理论应用于实践，加深理解。 该课件旨在帮助学习者掌握非正弦周期电路的分析技巧，这对于理解和设计现代电子系统至关重要。无论是工程师还是自学者，通过这个课程，他们可以提升对复杂信号处理和电路设计的理解能力。