HHT技术探讨:边际谱与EMD分析
需积分: 10 54 浏览量
更新于2024-07-24
收藏 2.11MB PDF 举报
"HHT精华讨论记录了HHT论坛上的重点问题,适合初学者学习,涵盖了Hilbert边际谱、EMD、HHT谱等相关话题,包括处理问题、代码示例和实践经验分享。"
HHT(Hilbert-Huang变换)是一种非线性、非平稳时间序列分析方法,由Huang等人提出,主要用于处理复杂动态系统的信号分析。其核心思想是通过经验模态分解(Empirical Mode Decomposition, EMD)将信号分解为一系列内在模态函数(IMF),然后再应用Hilbert谱分析。
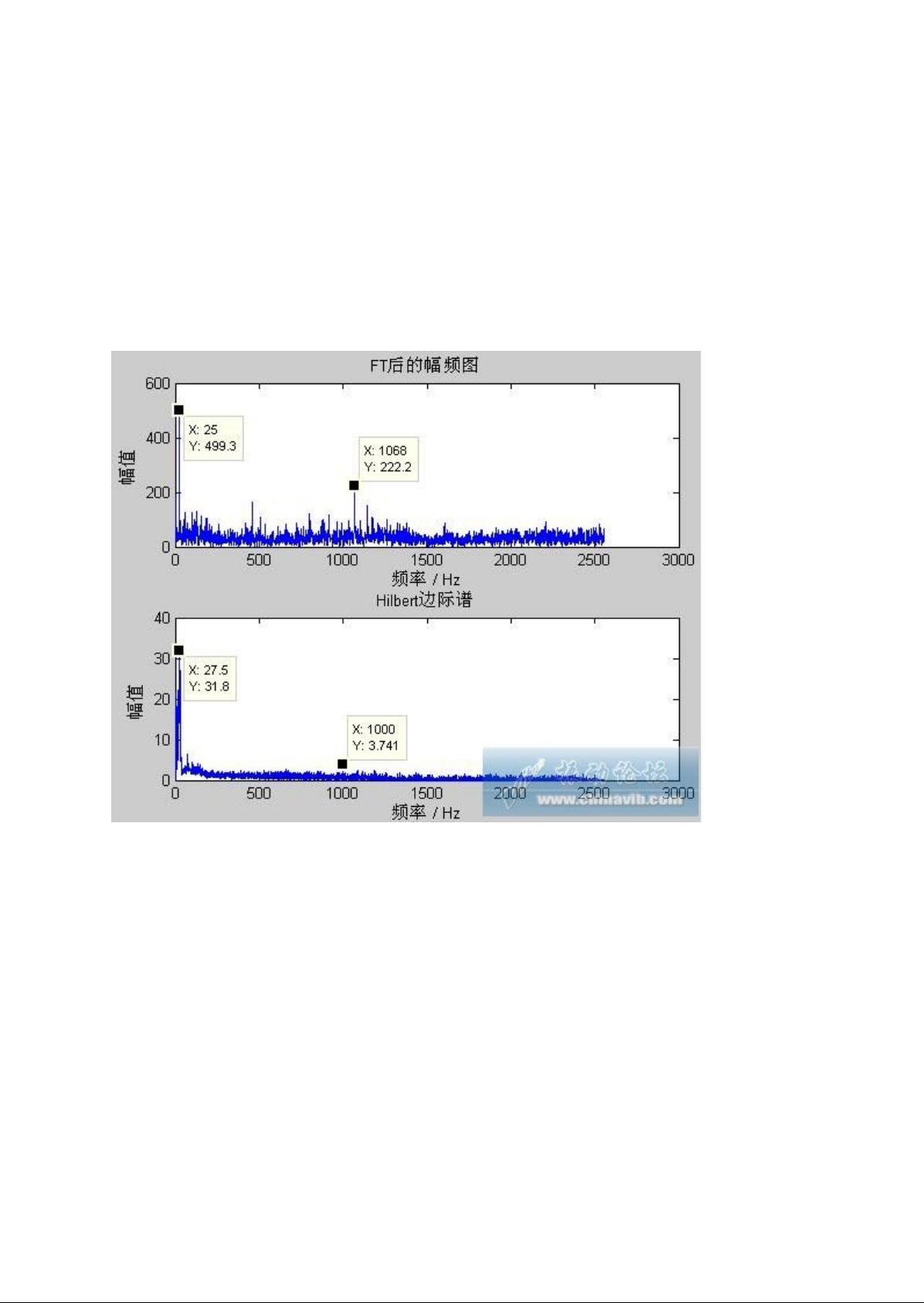
1、Hilbert边际谱:Hilbert边际谱是HHT的重要组成部分,它是通过对Hilbert变换得到的复包络进行积分而获得的。这个谱描述了信号的瞬时振幅与频率之间的关系,对于分析非线性、非平稳信号特别有用。在实践中,计算边际谱可能遇到精度问题,需要对代码进行优化。
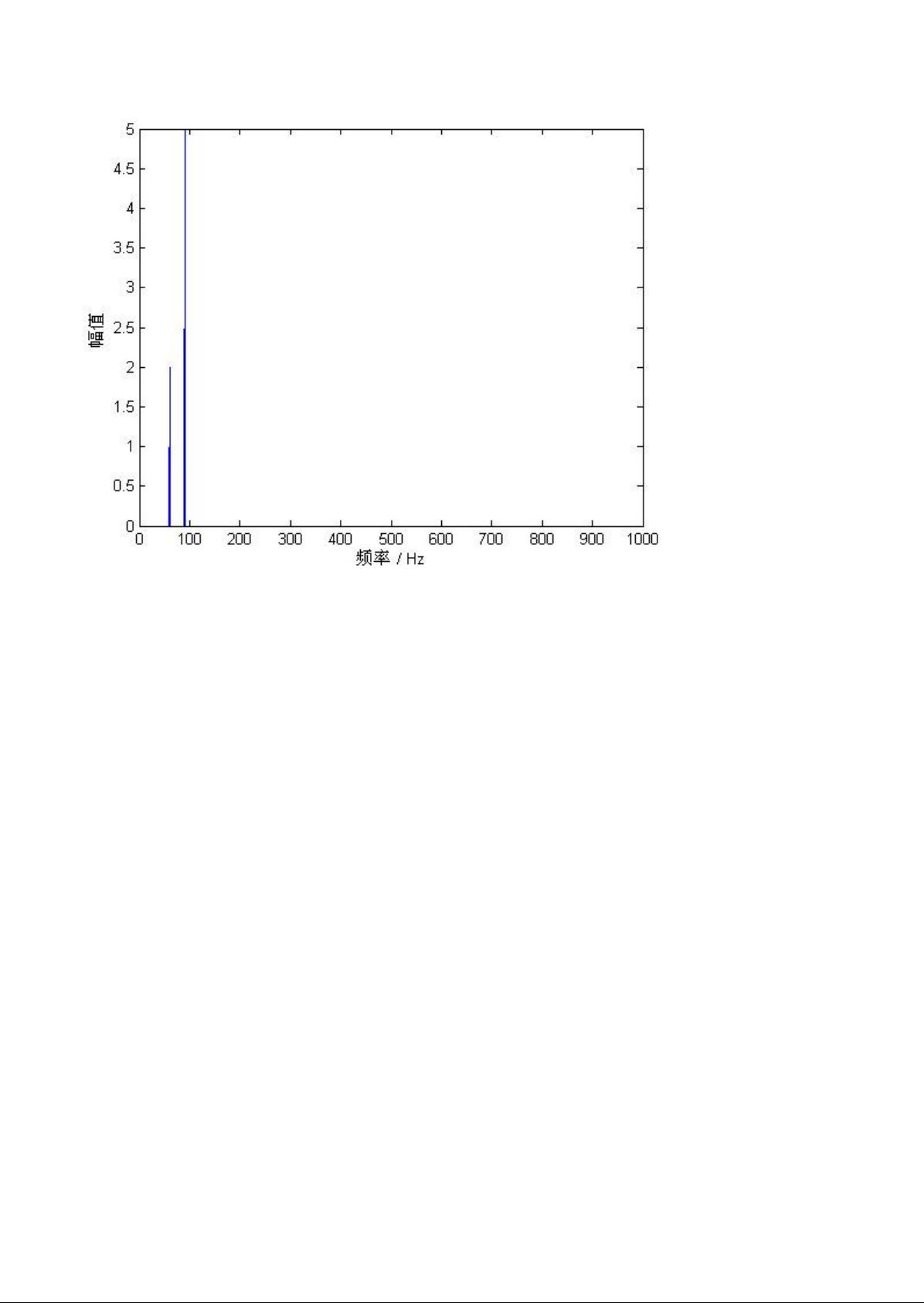
2、Hilbert谱和FT变换后的幅频谱:傅里叶变换(FFT)适用于平稳信号分析,但对非平稳信号处理效果不佳。HHT则能捕捉信号的时间局部特性,Hilbert谱提供的是瞬时频率信息,而FFT给出的是平均频率信息。
3、EEMD(Ensemble Empirical Mode Decomposition):EEMD是EMD的一个改进版本,通过噪声辅助的方式减少EMD的模态混合问题,提高分解的稳定性和准确性。
4、instfreq函数:用于计算IMF的瞬时频率,但在某些情况下可能会出现问题,需要谨慎处理。
5、EMD分解全过程:EMD通过迭代寻找信号的IMF,然后结合Hilbert变换得到Hilbert谱,整个过程对理解信号的动态特性至关重要。
6、调频信号分析:HHT和FFT在处理调频信号时会得出不同的结果,HHT能够揭示信号随时间变化的频率信息,而FFT则不能。
7-15、其他问题与实例:包括MATLAB代码实现、谱图问题、时频灰度谱转换、HHT谱的异常情况、实测信号处理等,这些都是HHT应用中常见的挑战和疑问,讨论提供了实践经验分享和解决办法。
这些讨论中的资源对学习和理解HHT及其应用非常有价值,尤其是对初学者,可以帮助他们掌握HHT的基本原理和实践技巧,解决在实际操作中可能遇到的问题。
2019-08-13 上传
2013-01-08 上传
2021-10-04 上传
点击了解资源详情
点击了解资源详情
2021-09-29 上传
2022-07-14 上传
2022-09-22 上传
tdnyb
- 粉丝: 1
- 资源: 9
最新资源
- JavaScript实现的高效pomodoro时钟教程
- CMake 3.25.3版本发布:程序员必备构建工具
- 直流无刷电机控制技术项目源码集合
- Ak Kamal电子安全客户端加载器-CRX插件介绍
- 揭露流氓软件:月息背后的秘密
- 京东自动抢购茅台脚本指南:如何设置eid与fp参数
- 动态格式化Matlab轴刻度标签 - ticklabelformat实用教程
- DSTUHack2021后端接口与Go语言实现解析
- CMake 3.25.2版本Linux软件包发布
- Node.js网络数据抓取技术深入解析
- QRSorteios-crx扩展:优化税务文件扫描流程
- 掌握JavaScript中的算法技巧
- Rails+React打造MF员工租房解决方案
- Utsanjan:自学成才的UI/UX设计师与技术博客作者
- CMake 3.25.2版本发布,支持Windows x86_64架构
- AR_RENTAL平台:HTML技术在增强现实领域的应用