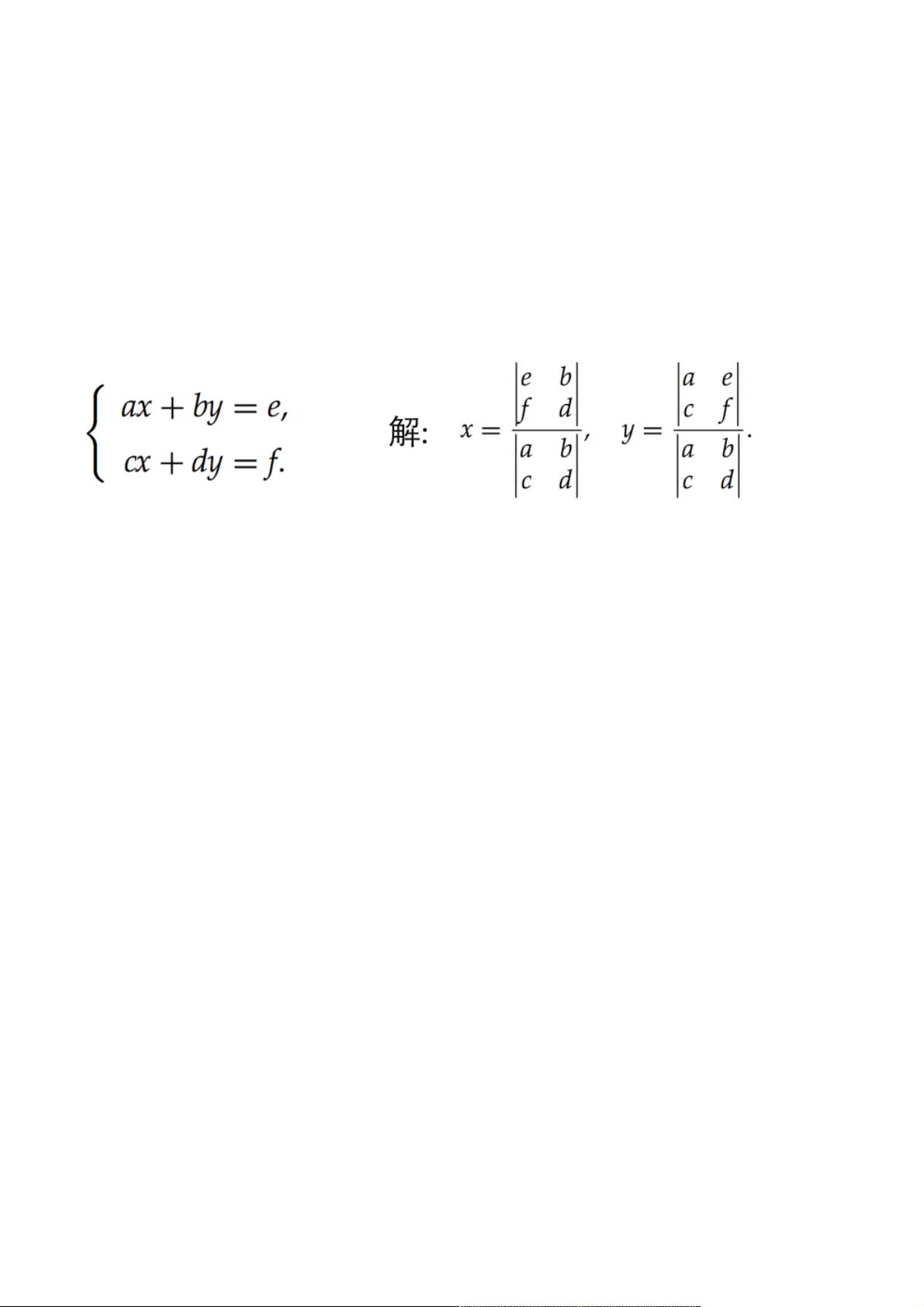js初级教程：三种高效寻找线段交点的算法详解

本文主要讲解了JavaScript中实现线段交点的三种算法，特别是针对初学者设计，旨在帮助理解和应用到实际编程中。首先，我们介绍的是**算法一：直线方程求交点**。该方法利用直线的一般方程 \( ax + by + c = 0 \)，其中\( a \), \( b \), \( c \) 是直线的系数，而不是线段端点。通过解这个线性方程组来找到潜在的交点坐标 \( (x, y) \)。如果线段的斜率不存在（即分母为0），意味着线段平行或共线，此时视为不相交。 接下来，通过比较交点 \( (x, y) \) 与线段端点的坐标关系，判断交点是否在线段上。如果交点满足 \( (x-a.x)(x-b.x) \leq 0 \) 和 \( (y-a.y)(y-b.y) \leq 0 \) 对于线段1，以及同样条件对于线段2，那么返回交点坐标。如果这些条件不满足，则说明交点不在任何一条线上，即线段不相交。 然而，算法一存在效率问题，因为它在计算交点之前没有先进行有效性检查，可能导致不必要的计算开销。为了优化性能，文章引入了**算法二：有效性判断**。这种方法首先通过计算两个线段斜率的差异（或方向向量的叉积）以及它们的长度（分母），来快速判断线段是否平行或重合。只有当两条线段不平行时，才进一步计算交点。这样避免了不必要的计算，并提高了算法效率。 此外，文章还提到了**第三种可能的方法**，虽然没有详细展示代码，但可以推测这是一种更高级的技术，可能是基于空间划分、数据结构优化或者几何变换的策略，旨在进一步减少计算复杂度和内存消耗，例如使用空间包围盒、线段树等数据结构辅助判断线段是否相交。 总结来说，本文详细介绍了两种常见的线段交点算法：一是通过一般方程求交点并判断有效性，二是优化后的有效性检测方法。初学者可以通过学习和实践这三种算法，提高自己的编程技能，特别是在处理图形和空间定位问题时。同时，对于性能要求更高的场景，还可以探索更复杂的算法优化技术。