小种群免疫遗传算法解决非线性区间值多目标优化
176 浏览量
更新于2024-08-26
收藏 942KB PDF 举报
本文主要探讨了"求解非线性区间值规划的多目标免疫遗传算法"这一研究领域。在当前的工程应用人工智能背景下，特别是67卷第235-245页的文章中，作者Zhuhong Zhang、Xiaoxia Wang和Jiaxuan Lu聚焦于处理一般无约束的多目标区间值优化问题。他们的研究关注于在小规模种群环境中应用免疫遗传算法，这是一种特殊的优化策略，旨在提高效率和效果的平衡。
核心概念包括：
1. 非线性区间值规划：非线性问题通常涉及函数的非线性关系，而区间值规划则在此基础上增加了不确定性，每个目标函数都有可能在给定区间的范围内取值，而非精确的单一值。
2. 多目标免疫遗传算法：与单目标优化不同，多目标优化关注的是多个目标之间的权衡，而不是单一最优解。免疫遗传算法借鉴了免疫系统的选择和适应机制，结合遗传算法的搜索策略，寻找一个多目标问题的满意解集，即帕累托最优解。
3. 区间算术规则和可能性模型：这两种工具被用来评估和区分个体的性能，确保算法能够理解和处理区间内的变化和不确定性。
4. 拥挤度模型：在区间值环境下，开发了一个拥挤度模型，用于筛选出多余或相似的个体，以保持种群多样性，避免过度集中。
5. 种群分类与免疫进化：种群被划分为不同的类别，以便引导不同的个体向特定方向发展。免疫进化机制则有助于保持算法的动态性和灵活性，同时精英个体通过遗传进化来探索关键区域。
6. 计算复杂度：理论分析指出，算法的计算复杂度主要依赖于精英人口的数量，这对于设计高效的优化过程至关重要。
7. 实验比较：研究结果通过与其他方法的对比，展示了该算法在保持解决问题效率的同时，具有良好的性能和解决多模态及硬多目标区间值编程问题的能力。
这篇文章是一项针对复杂优化问题的创新研究，提供了有效的多目标区间值规划解决方案，适用于实际工程应用中的挑战，特别是在大数据和信息工程领域。
Z. Zhang et al. Engineering Applications of Artificial Intelligence 67 (2018) 235–245
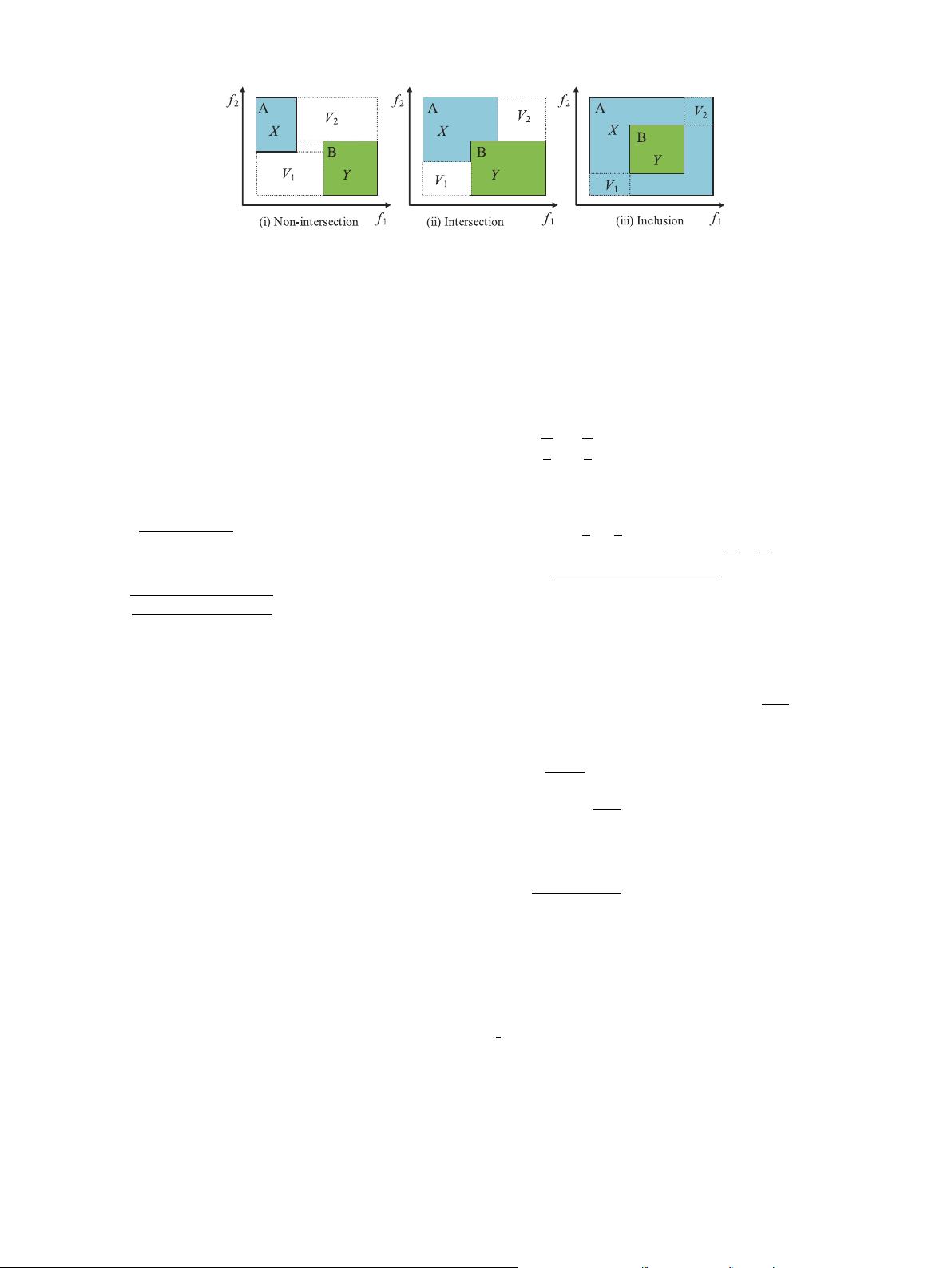
Fig. 1. The relationship between hypercubes of two candidates.
We here introduce the following weak comparison relation between 𝐴
and 𝐵,
𝐴 ≤ 𝐵 ⟺ 𝐴
𝑅
≤ 𝐵
𝐿
, 𝐴 ≥ 𝐵 ⟺ 𝐵 ≤ 𝐴. (2)
Generally speaking, it is not true that 𝐴 − 𝐴 = 0, for example when
A=[−2,2], we can see that A-A=[−4,4]. Thus, we here prescribe that
𝐴 equals 𝐵 if and only if 𝐴
𝐿
= 𝐵
𝐿
and 𝐴
𝑅
= 𝐵
𝑅
. This way, Eq. (2)
indicates that once 𝐴 ≤ 𝐵 and 𝐵 ≤ 𝐴, 𝐴 and 𝐵 will degenerate to 𝑎,
i.e., [𝑎, 𝑎]. It is emphasized that, when 𝐴 ∩ 𝐵 ≠ 𝜙 and 𝐴 ≠ 𝐵, Eq. (2)
cannot be adopted to execute comparison between 𝐴 and 𝐵. In such
case, the version of possibility degree is an alternative way to compare
𝐴 with 𝐵. We here cite the following possibility degree model (Zhou
and Liu, 2008),
𝑃 𝑟{𝐴 ≤ 𝐵} =
𝑑(𝐴, 𝐶)
𝑑(𝐴, 𝐶) + 𝑑(𝐵, 𝐶)
, (3)
where 𝐶 = [𝐶
𝐿
, 𝐶
𝑅
], 𝐶
𝑅
= max Γ and 𝐶
𝐿
= max Γ ⧵ {𝐶
𝑅
} with
Γ = {𝐴
𝐿
, 𝐴
𝑅
, 𝐵
𝐿
, 𝐵
𝑅
}, and meanwhile
𝑑(𝐴, 𝐶) =
(𝐴
𝐿
− 𝐶
𝐿
)
2
+ (𝐴
𝑅
− 𝐶
𝑅
)
2
2
. (4)
Based on Eq. (3), Zhou and Liu (2008) introduced the version of
individual dominance. In other words, 𝐱 dominates 𝐲 (𝐱 ≺ 𝐲) if 𝜎
𝑖
(𝐱, 𝐲) ≥
𝜎
𝑖
(𝐲, 𝐱) for any 𝑖 with 1 ≤ 𝑖 ≤ 𝑚, and there exists 𝑖
0
such that 𝜎
𝑖
0
(𝐱, 𝐲) >
𝜎
𝑖
0
(𝐲, 𝐱), where
𝜎
𝑖
(𝐱, 𝐲) = 𝑃 𝑟{𝑓
𝑖
(𝐱, 𝑈 ) ≤ 𝑓
𝑖
(𝐲, 𝑈 )}. (5)
Naturally, 𝐱
∗
is said to be a Pareto optimal solution of the above MIVP if
there does not exist 𝐲 in 𝐷 such that 𝐲 ≺ 𝐱
∗
. In order to identify whether
one individual is superior to another one in a given population 𝐴 with
size 𝑁, we introduce the following computational model to compute the
rank of individual 𝐱 in 𝐴,
𝑅(𝐱) = 𝑁 − {𝐲 ∈ 𝐴𝐲 ≺ 𝐱}, (6)
where Λrepresents the number of elements in set Λ. Eq. (6) indicates
that 𝐱 is better if 𝑅(𝐱) is larger, and especially it is a non-dominated
individual in 𝐴 if 𝑅(𝐱) = 𝑁 . This way, 𝐴 may be divided into two sub-
populations. One is composed of non-dominated individuals in 𝐴, the
other consists of those dominated ones.
Remark 1. When computing the ranks of all individuals in 𝐴, we
first need to calculate the possibility degrees of sub-objective interval
numbers for any two individuals through Eq. (3), for which the total of
executions is 𝑚𝑁
2
. Second, we also execute 𝑚𝑁
2
comparisons between
individuals through non-dominated sorting. Once all the non-dominated
individuals in 𝐴 need to be discriminated, the computational complexity
is 𝑂(𝑚𝑁
2
).
4. Crowding degree model
As we know, the objective interval vectors of individuals 𝐱 and 𝐲,
i.e., 𝑓 (𝐱, 𝑈) and 𝑓 (𝐲, 𝑈), correspond to two hypercubes in the objective
space. In general, their possible position relations, given by Fig. 1
include non-intersection, intersection and inclusion. In the above figure,
𝑋 and 𝑌 denote the hypercubes of interval objective vectors 𝑓 (𝐱, 𝑈 )
and 𝑓 (𝐲, 𝑈 ) for candidates 𝐱 and 𝐲, respectively; A and B represent the
vertexes of 𝑋 and 𝑌 at the top-left corner, respectively; 𝑉
1
and 𝑉
2
stand
for the hypervolumes of the corresponding dash hypercubes. Let 𝑉
𝑥𝑦
be
the hypervolume of the outer hypercube. In this way, 𝑉
1
, 𝑉
2
and 𝑉
𝑥𝑦
can
be represented by the endpoints of the interval-valued sub-objectives,
𝑉
1
=
𝑚
𝑖=1
𝑓
𝑖
(𝐱) − 𝑓
𝑖
(𝐲),
𝑉
2
=
𝑚
𝑖=1
𝑓
𝑖
(𝐱) − 𝑓
𝑖
(𝐲),
𝑉
𝑥𝑦
=
𝑚
𝑖=1
(𝑐
𝑖
− 𝑑
𝑖
),
(7)
where 𝑐
𝑖
= max{𝑓
𝑖
(𝐱), 𝑓
𝑖
(𝐲)} and 𝑑
𝑖
= min{𝑓
𝑖
(𝐱), 𝑓
𝑖
(𝐲)}. Additionally, the
distance between A and B is defined by
𝑑(𝐱, 𝐲) =
𝑚
𝑖=1
(𝑚(𝑓
𝑖
(𝐱, 𝑈 )) − 𝑚(𝑓
𝑖
(𝐲, 𝑈 )))
2
,
(8)
where 𝑚(𝑓
𝑖
(𝐱, 𝑈 )) denotes the midpoint of interval 𝑓
𝑖
(𝐱, 𝑈 ). Although
Eq. (8) can present the degree of approximation of points A and B,
it cannot completely reflect the relation between the two hypercubes.
Once we move the positions of 𝑋 and 𝑌 , the values of 𝑉
1
, 𝑉
2
, 𝑉
𝑥𝑦
and
𝑑(𝐱, 𝐲) will make change correspondingly, but
𝑉
1
+𝑉
2
2𝑉
𝑥𝑦
only does minor
change. This way, the crowding degree of 𝐱 and 𝐲 in the objective space
can be defined here by
𝐷(𝐱, 𝐲) =
𝑉
1
+ 𝑉
2
2𝑉
𝑥𝑦
𝑑(𝐱, 𝐲). (9)
Again, since 0 ≤
𝑉
1
+𝑉
2
𝑉
𝑥𝑦
< 1, 𝐷(𝐱, 𝐲) changes within 0 and 𝑑(𝐱, 𝐲). Eq.
(9) hints that if 𝑋 and 𝑌 are close, 𝐷(𝐱, 𝐲) is small. Therefore, in order
to reflect the diversity of a given population 𝑃 , the crowding degree of
individual 𝐱 in 𝑃 is designed by
𝐶(𝐱) =
𝐷(𝐲, 𝐱) + 𝐷(𝐱, 𝐳)
2
(10)
where 𝐲 and 𝐳 are two closest individuals of 𝐱 in 𝑃 . Eq. (10) illustrates
that, if the crowding degrees of individuals in 𝑃 are small, these
individuals will have high similarity and thus weak population diversity.
Remark 2. In order to compute the crowding degrees of individuals
in 𝑃 with size 𝑁, the two closest individuals of each individual in
the objective space are first decided, for which we need to execute
(
1
2
𝑁(𝑁 − 1) + 𝑁𝑙𝑜𝑔𝑁 ) times. Thus, once Eq. (10) is enforced in 𝑃 , it
will cause the complexity of 𝑂(𝑁
2
).
5. Algorithm formulation and design
Based on the above designs, immune inspirations and also additive
genetic operators, we in this section formulates MIIGA, for which
the flowchart is given in Fig. 2. One such approach includes three
functional modules, i.e., population division, immune evolution and
237
剩余10页未读，继续阅读
2022-03-29 上传
2021-12-08 上传
点击了解资源详情
2022-07-15 上传
2019-09-12 上传
2022-10-16 上传
2022-10-16 上传
点击了解资源详情
点击了解资源详情
weixin_38545923
- 粉丝: 4
- 资源: 933
我的内容管理
展开
最新资源
- 火炬连体网络在MNIST的2D嵌入实现示例
- Angular插件增强Application Insights JavaScript SDK功能
- 实时三维重建：InfiniTAM的ros驱动应用
- Spring与Mybatis整合的配置与实践
- Vozy前端技术测试深入体验与模板参考
- React应用实现语音转文字功能介绍
- PHPMailer-6.6.4: PHP邮件收发类库的详细介绍
- Felineboard：为猫主人设计的交互式仪表板
- PGRFileManager：功能强大的开源Ajax文件管理器
- Pytest-Html定制测试报告与源代码封装教程
- Angular开发与部署指南：从创建到测试
- BASIC-BINARY-IPC系统：进程间通信的非阻塞接口
- LTK3D: Common Lisp中的基础3D图形实现
- Timer-Counter-Lister:官方源代码及更新发布
- Galaxia REST API：面向地球问题的解决方案
- Node.js模块：随机动物实例教程与源码解析
