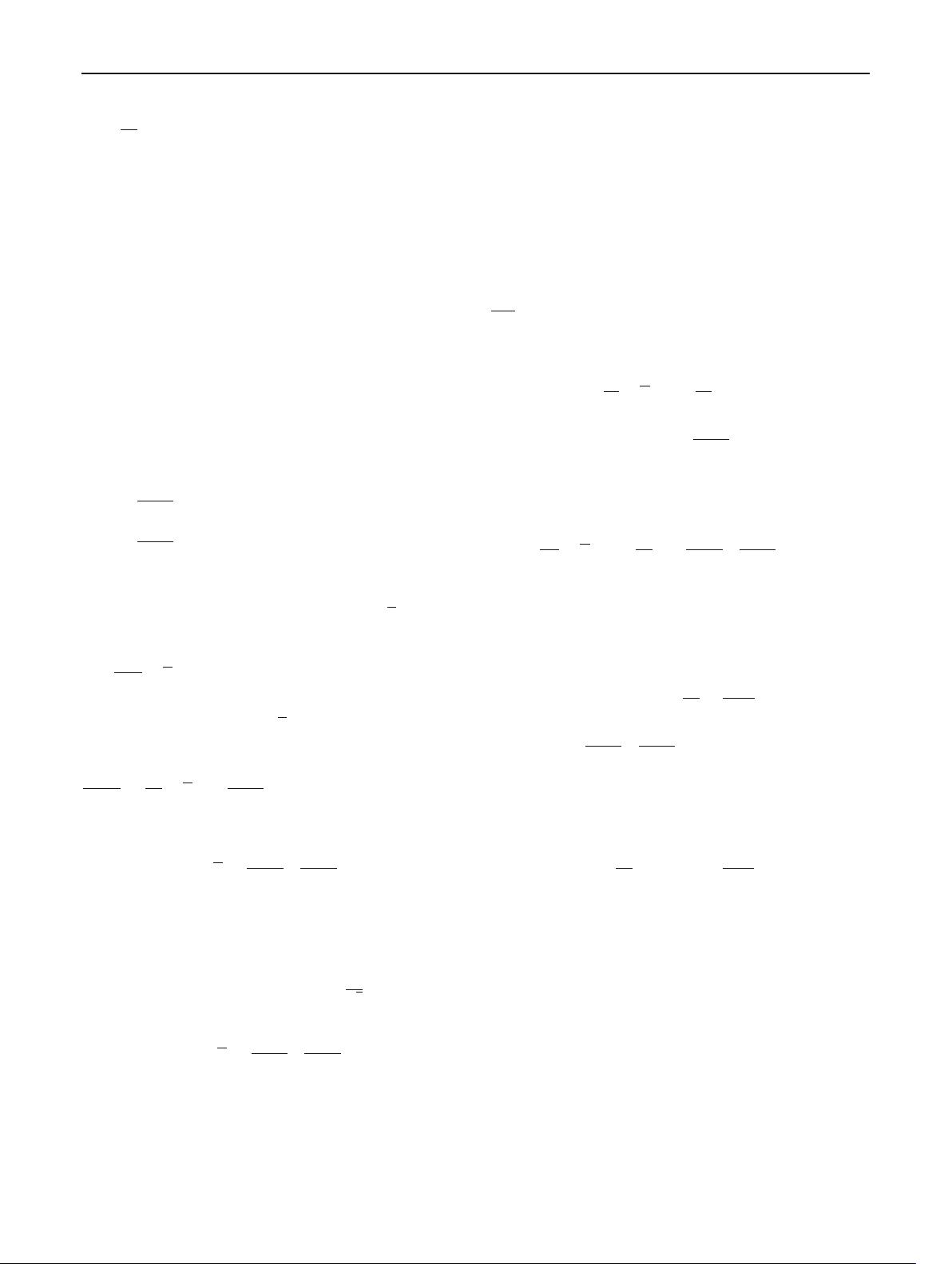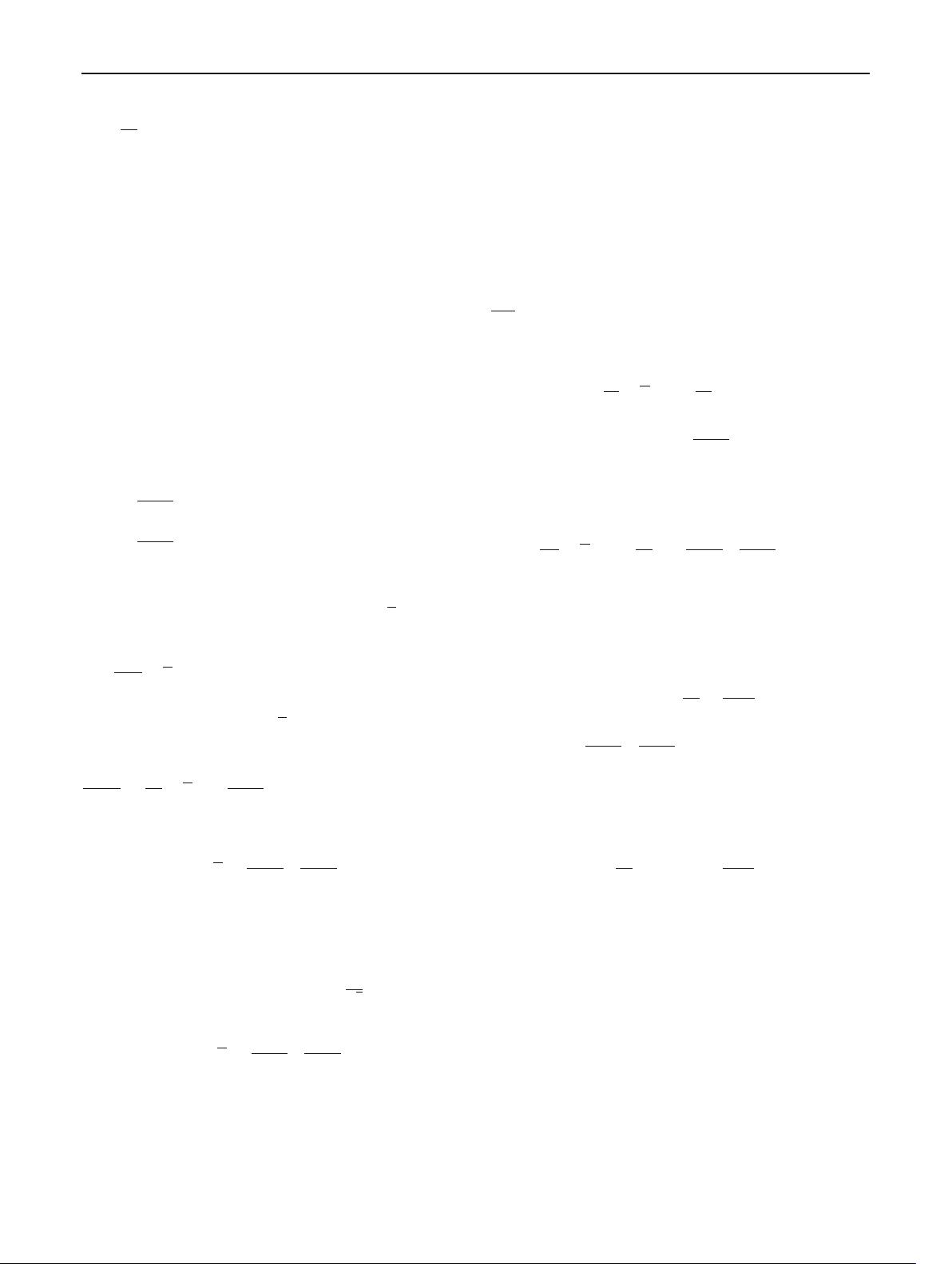
Eur. Phys. J. C (2015) 75 :107 Page 3 of 11 107
We assume that the volume charge density has the form
σ(r)e
λ(r)
2
= σ
0
r
n
, (12)
where n is an arbitrary constant and σ
0
is the central charged
density. Though it is true that one is free to choose an infinite
number of possible ansatz, the main motivation for a particu-
lar choice in our model was to generate solutions which could
be considered as physically meaningful. Secondly, solutions
obtained earlier for the neutral case can easily be regained
from our solution for the specified ansatz. This enables one
to investigate the effects of electromagnetic field on the sys-
tem explicitly. The choice (12) of the charge density is only
dictated by the mathematical convenience and has no physi-
cal justification since it gives the energy divergent at infinity.
However, this particular choice is different from the Gaus-
sian distribution of charge assumed in Ref. [18]. We will see
that solutions obtained earlier for the neutral case can easily
be regained from our solution for the specified ansatz.
Consequently, from Eq. (11) we get
E(r ) =
4πσ
0
n + 2
r
n+1
, (13)
q(r) =
4πσ
0
n + 2
r
n+2
. (14)
Further, we consider the maximally localized source of
energy of the static spherically symmetric charge distribution
as a Gaussian distribution with minimal width
√
θ expressed
as [19],
ρ =
M
4πθ
e
−
r
2
4θ
, (15)
where M is the total mass of the source diffused throughout
a region of linear dimension
√
θ.
Substituting (13) and (15)in(7), we obtain
λ
e
−λ
2r
=
M
2θ
e
−
r
2
4θ
+
4πσ
0
n + 2
2
r
2n+2
+ , (16)
which, on integration, yields
e
−λ
=−A + 2Me
−
r
2
4θ
−
1
n + 2
4πσ
0
n + 2
2
r
2n+4
− r
2
,
(17)
where A is a constant of integration. In Ref. [9] it has been
shown that the constant of integration A plays the role of the
mass of the black hole, i.e., A = M. In our construction,
if we set σ
0
= 0 and consider the limit
r
√
θ
→∞, then it
follows that A = M. Accordingly, we rewrite Eq. (17)as
e
−λ
=−M + 2Me
−
r
2
4θ
−
1
n + 2
4πσ
0
n + 2
2
r
2n+4
− r
2
.
(18)
Note that the vacuum Einstein field equations in (2 + 1)-
dimensional spacetime in the presence of a negative cos-
mological constant ( < 0) admit a black hole solution
known as BTZ [7] solution for which we have g
rr
=
(
g
tt
)
−1
.
To retain the structure of BTZ black hole, we must have
e
ν
= e
−λ
.FromEqs.(7)–(8), it then follows that
p
r
=−ρ, (19)
which is the ‘ρ vacuum’ EOS in reference to ‘zero-point
energy of quantum fluctuations’ [19].
Combining Eqs. (7)–(9) and (19), we obtain
e
−λ
2
(λ
2
− λ
) = 2π p
t
+ E
2
− . (20)
From Eq. (16), we get
e
−λ
(λ
− λ
2
) =
M
θ
e
−
r
2
4θ
1 −
r
2
2θ
+2(2n + 3)
4πσ
0
n + 2
2
r
2n+2
+ 2.
(21)
Combining Eqs. (20) and (21), we obtain
p
t
=−
M
πθ
e
−
r
2
4θ
1 −
r
2
2θ
−
n + 2
π
4πσ
0
n + 2
2
r
2n+2
.
(22)
We, thus, have a noncommutative geometry inspired analytic
model of a 3-D charged black hole. In this construction, the
spacetime near the origin behaves as
e
ν
= e
−λ
=−M + 2M
1 −
r
2
4θ
+
r
4
32θ
2
+ O(r
8
)
−
1
n + 2
4πσ
0
n + 2
2
r
2n+4
− r
2
. (23)
Note that, for n = 0, by adjusting the parameters suitably,
one can regain the spacetime for the (2 + 1)-dimensional
static charged distribution
e
ν
= e
−λ
= M −
M
2θ
+
r
2
+
2M
32θ
2
− 2π
2
σ
2
0
r
4
,
(24)
obtained earlier by Liang and Liu [20].
In the following sections, we shall analyze some features
of our charged BTZ black hole.
3 Features of the charged BTZ black hole
3.1 Formation of event horizons
The condition for the formation of event horizon is given by
g
tt
(r
h
) = 0, which implies
123