支持向量机详解：从线性到非线性，核函数应用

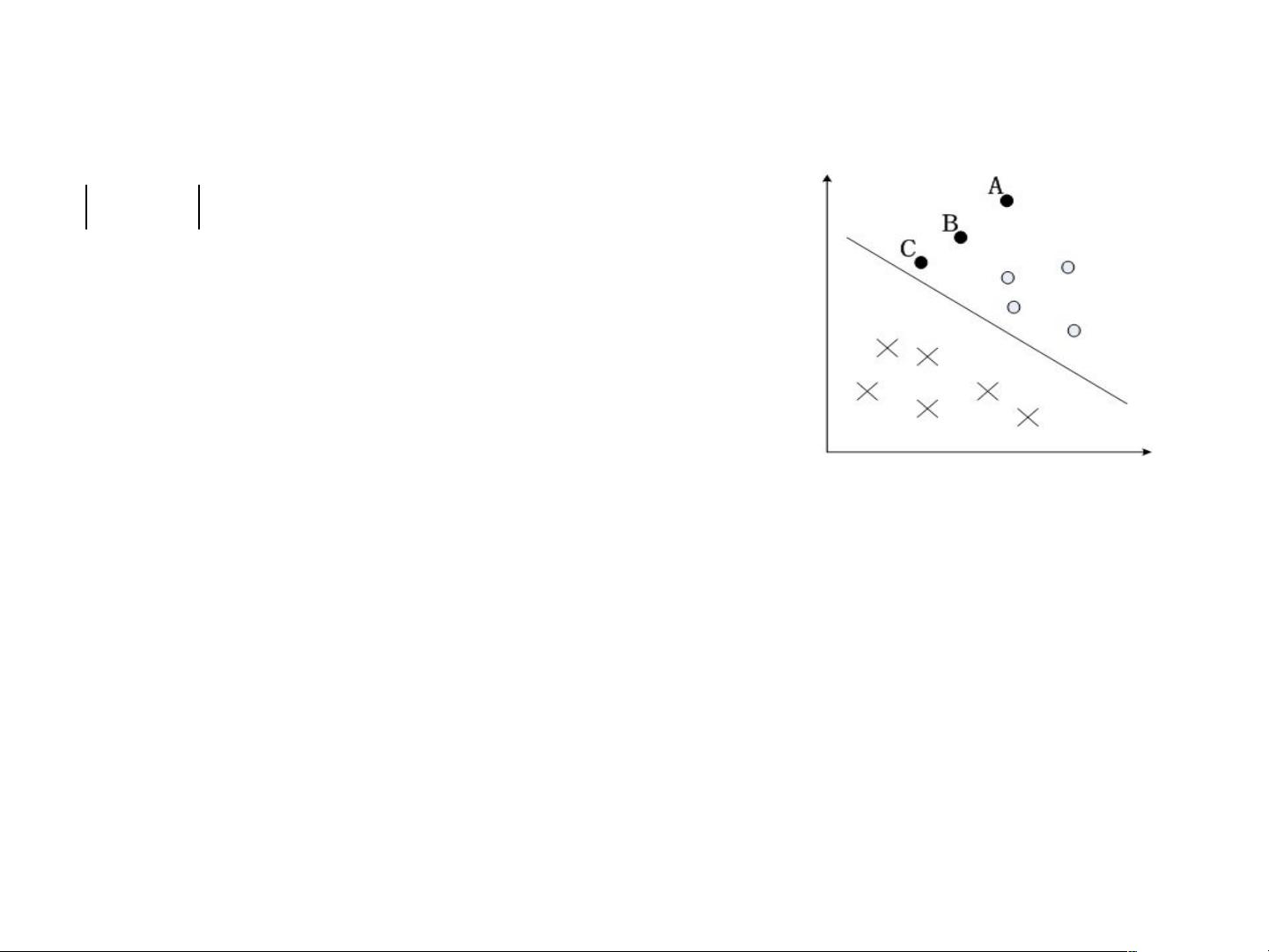
"本文主要介绍了支持向量机（SVM），一种广泛应用的机器学习模型，尤其在分类和回归任务中表现出色。SVM的核心思想是找到一个能够最大程度地分离两类样本的超平面，以实现最佳分类效果。" 支持向量机（Support Vector Machine，简称SVM）是一种监督学习算法，它在分类问题中寻找一个最优的决策边界，以最大化不同类别之间的间隔。最初，SVM被设计用于处理线性可分的数据集，但后来发展出非线性分类能力，通过引入核函数来处理非线性问题。 在线性可分的情况下，支持向量机的目标是找到一个能最大化“几何间隔”的超平面。几何间隔是指样本点到超平面的实际距离，它考虑了超平面的法向量和实例点的坐标。如果一个超平面关于某个样本点的几何间隔为正，并且该点的分类标签与超平面的分类方向一致，那么这个样本点就被正确分类。函数间隔是几何间隔的标度版本，考虑了超平面的系数，其值等于几何间隔乘以超平面的权重向量的模。 支持向量机的学习算法可以分为两个主要步骤：首先，构造一个优化问题，目标是找到最大化几何间隔的超平面，这通常通过解决一个凸二次规划问题来实现；其次，根据求解的结果，得到分类决策函数。在处理线性可分数据时，存在一个最大间隔的分离超平面，并且它是唯一的。这一特性使得SVM在理论和实践中都具有很好的稳定性。 在面对线性不可分的数据时，SVM引入了“软间隔最大化”概念，允许一定数量的样本点落在决策边界内，同时引入松弛变量来衡量这些错误分类的代价。这样，模型可以容忍一定程度的误分类，以达到更好的全局分类效果。 非线性支持向量机是通过核技巧实现的，核函数能够将原始特征空间映射到高维特征空间，在这个新的空间中原本难以分离的样本可能变得线性可分。常用的核函数有线性核、多项式核、高斯核（RBF）等，它们在保持计算效率的同时，赋予SVM处理复杂非线性问题的能力。 支持向量机的一个关键优势在于它的简洁性，决策函数只依赖于部分样本点，即支持向量，而非所有数据点。这使得SVM在小样本和高维数据上表现良好，而且训练时间相对短。 支持向量机是一种强大的机器学习工具，尤其适用于处理分类问题。通过理解和支持向量机的基本原理，如线性可分支持向量机、软间隔最大化、核函数等，我们可以有效地构建和应用SVM模型来解决实际问题。