系统聚类法详解与Matlab实现

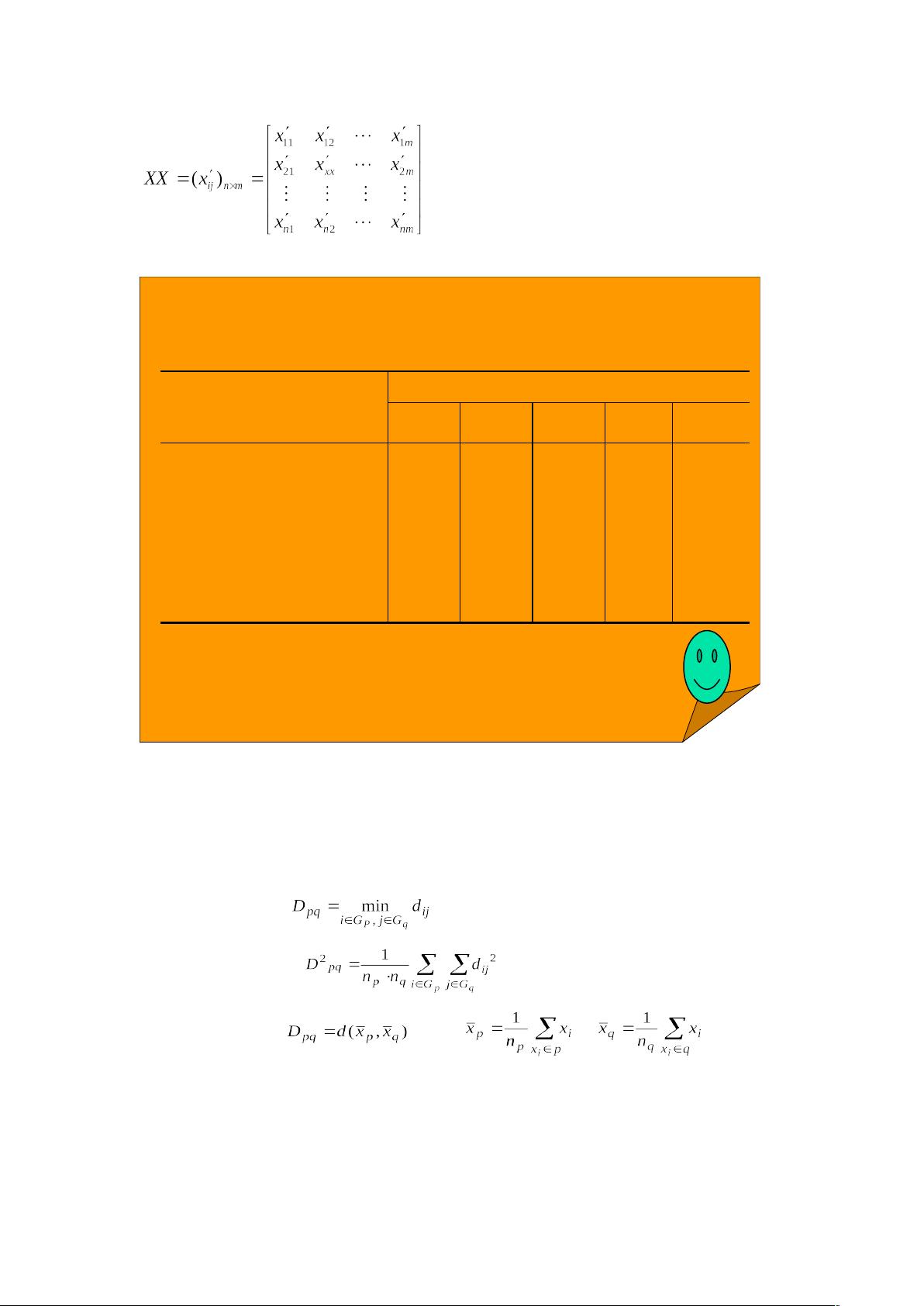
"系统聚类法是一种常用的聚类分析方法，它通过计算样本间的距离来进行无监督的分类。本文详细介绍了系统聚类法的概念、步骤以及如何使用Matlab软件进行实现。聚类分析广泛应用于各个领域，如考古、地质、天气预报等，它通过寻找样本之间的相似性来构建类别。在系统聚类法中，每个分类对象被视为一个样品，通过选定的特征变量测量其属性。数据矩阵是分析的基础，其中包含所有样品的特征变量观测值。计算样品之间的距离是关键，常用的有Minkowski距离，包括绝对值距离、欧氏距离和切比雪夫距离。当特征变量的尺度和单位不同时，需要进行预处理以确保距离计算的公正性。" 系统聚类法是一种在没有先验知识的情况下，对大量样品进行分类的统计方法。这种方法依赖于样品之间的相似度，通常以距离作为衡量标准。在系统聚类过程中，首先计算每对样品之间的距离，然后根据这些距离信息构建样品的分类树（dendrogram）。系统聚类法通常包括以下几个步骤： 1. **数据准备**：确定样品和特征变量，测量每个样品的特征变量值，形成样本资料矩阵。 2. **距离计算**：使用合适的距离度量方法（如Minkowski距离）计算所有样品对之间的距离。Minkowski距离包括三种特殊情况：[pic] = 1对应曼哈顿距离（Cityblock distance），[pic] = 2对应欧几里得距离，[pic] = ∞对应切比雪夫距离。 3. **相似性矩阵构建**：基于计算出的距离，构建样品之间的相似性矩阵，通常采用的是距离的逆或者倒数。 4. **归并策略**：选择两个最近的样品或类别进行合并，更新相似性矩阵，然后重复此过程，直到所有样品都合并为一个类别，或者达到预设的类别数。 5. **形成分类树**：通过记录每次归并的顺序，可以构建出一个层次结构的分类树，表示样品之间的关系。 在Matlab中实现系统聚类，可以调用`linkage`函数，该函数接受样本矩阵和距离度量方法作为输入，返回一个链接矩阵，描述了样品之间的关系。然后，可以使用`dendrogram`函数绘制分类树。为了更好地处理不同尺度的特征，可能需要进行标准化或归一化操作，如使用`zscore`或`normality`函数。 此外，还需要注意一些实际应用中的问题，例如选择合适的距离度量、处理异常值、确定最佳类别数等。在实践中，可能需要结合领域知识和可视化工具来优化分类结果。最后，上机作业可能包括根据给出的数据集应用系统聚类法，分析结果并解释分类结构。 系统聚类法是一种强大的数据分析工具，通过Matlab的函数支持，可以方便地应用于各种数据集，帮助研究人员和分析师探索数据的内在结构和模式。