FFT算法解析：性能与应用

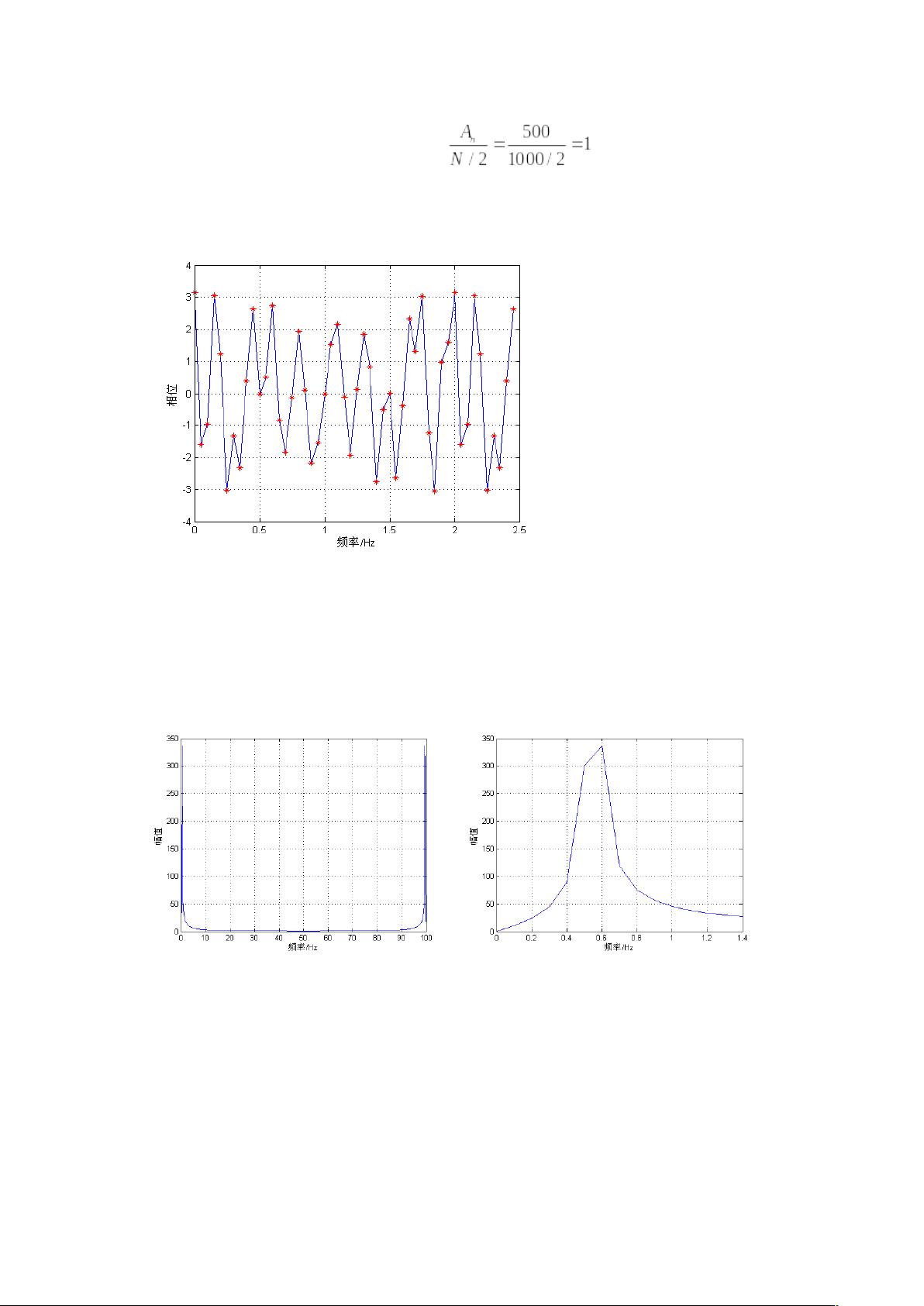
"FFT算法在处理振荡信号时，主要关注其速度、精度以及提高精度的方法。快速傅里叶变换（FFT）是一种高效计算离散傅里叶变换（DFT）的算法，对于N点序列，无论是实数还是复数，它会生成一个N点复数序列。每个点对应一个频率，模值表示该频率下的幅度，相位则表示该频率下的信号相位。FFT的频率分辨率取决于采样频率Fs和采样点数N，分辨率等于Fs/N。为了提高频率分辨力，可以增加采样点数或提升采样频率。 当处理衰减信号时，FFT可能无法提供准确的幅值，尽管仍可正确识别频率。在这种情况下，可以结合半功率点法来估算信号的阻尼比。FFT的计算复杂度为O(Nlog2N)，在实际应用中，如使用Matlab的FFT函数，即使是处理100k点的序列，所需时间也仅为0.03秒左右，显示出FFT的高效性能。 对于标准信号分析，如余弦信号，通过FFT可以精确地确定信号的频率成分。例如，分析一个10秒长，频率为0.5Hz的余弦信号，FFT结果会在0.5Hz处显示出峰值，幅值为1，相位为0。采样频率为100Hz，分析数值通常只关注低于采样频率一半的部分，因为FFT结果具有对称性。" 在深入理解FFT算法性能时，有几个关键点需要强调： 1. 频率分辨率：频率分辨率是FFT能够分辨的最小频率差，它与采样频率Fs成反比，与采样点数N成正比。增加采样点数或提高采样频率可以提高频率分辨率，从而更好地辨识信号中的不同频率成分。 2. 幅度与相位：FFT结果中的每个点代表一个特定频率的幅度和相位。幅度反映了信号在该频率的强度，而相位提供了关于信号相位偏移的信息。 3. 衰减信号的处理：由于FFT基于离散样本，对于衰减信号，尤其是非线性衰减，可能会导致幅度估计不准确。因此，对于这类信号，需要结合其他方法如半功率点法来估计信号的阻尼比，以获得更全面的分析结果。 4. 计算效率：FFT算法的效率体现在其时间复杂度上，为O(Nlog2N)，远优于直接计算DFT的O(N^2)复杂度。这使得FFT成为实时信号处理和大数据分析的首选工具。 5. 标准信号分析：通过FFT可以精确分析已知信号的频谱特性，例如标准的正弦或余弦波。通过对结果进行适当的放大和分析，可以找到信号的主要频率成分及其相位。 6. 采样原则：遵循奈奎斯特定理，确保采样频率至少是信号最高频率的两倍，以避免混叠现象。在分析结果中，通常只关注0到Fs/2的部分，因为这部分包含了所有可能的正频率成分。 FFT算法在处理振荡信号时展现出高速度和高精度的特点，但在处理衰减信号时需结合其他方法以提高幅值估计的准确性。理解和掌握这些知识点，对于在信号处理和频谱分析领域的工作至关重要。