FPGA上的LDPC解码器：一项综合调查

需积分: 9 127 浏览量更新于2024-07-19 收藏 3.6MB PDF 举报

"A Survey of FPGA-Based LDPC Decoders" 这篇论文深入探讨了基于FPGA（Field-Programmable Gate Array，现场可编程门阵列）的低密度奇偶校验（Low-Density Parity Check，LDPC）解码器的设计关键因素，并对当前文献进行了广泛的回顾。LDPC解码器在通信系统中广泛应用，因其出色的错误校正性能和适合并行硬件实现而受到青睐。研究者们投入大量精力设计能充分利用FPGA灵活性、高速处理能力和并行性的LDPC解码器。 FPGA设备在设计原型和小批量生产设备制造方面具有优势，因为它们的在系统可编程性使得其成本效益远超ASIC（Application-Specific Integrated Circuit，专用集成电路）。然而，公开文献中发布的FPGA基LDPC解码器设计在设计选择和性能指标上存在很大差异，这使得对比分析变得困难。论文对140个已发表的设计（包括学术界和工业界的）进行了深入比较，分析了相关性能权衡，并指出了七个关键性能特征： 1. 处理吞吐量：衡量解码器在单位时间内可以处理的数据量。 2. 处理延迟：从接收到数据到完成解码所需的时间。 3. 硬件资源需求：解码器所需的逻辑资源，如逻辑单元、存储器等。 4. 错误校正能力：解码器能够纠正的错误程度或错误率。 5. 处理能量效率：解码器在执行任务时的功耗与性能之间的关系。 6. 带宽效率：解码器利用输入/输出带宽的能力。 7. 灵活性：解码器适应不同编码参数或操作条件的能力。论文提供了一些建议，以促进未来设计的公平比较，并为改进FPGA基LDPC解码器的设计提供了机会。这些设计不仅涉及技术层面，还涵盖了算法优化、资源分配和架构创新等多个方面，旨在提升解码器的性能和效率。通过对这些性能特性的分析，研究人员和工程师能够更好地理解各种设计决策的影响，从而推动LDPC解码器技术的进一步发展。

IEEE COMMUNICATIONS SURVEYS AND TUTORIALS 5

achieves a strong error correction capability is a complex task,

so this is usually the ﬁrst aspect of the code to be designed.

Following this, the generator matrix G can be derived from

H, by following the reverse of the process described above.

3) Factor graphs: The PCM H can also be visualised

graphically using a factor graph, which is also known as a

Tanner graph [18]. This is exempliﬁed in Fig. 4 for the PCM

of (13). A factor graph is comprised of two sets of connected

nodes, namely N Variable Nodes (VNs) for representing the

columns of H and M Check Nodes (CNs) for representing

the rows.

Variable nodes

Edges

Check nodes

˜q

4−1

˜r

4−9

Fig. 4. A factor graph for an example LDPC code

The connections

above each VN in Fig. 4 pertain to

LLRs associated with the N codeword bits of ˆc. An edge

connects the i-th VN v

to the j-th CN c

if there is a non-

zero element in the i-th column and j-th row of H, H

= 1.

To illustrate this, all of the edges that are connected to the 1

CN c

in Fig. 4 are shown with thicker lines. These edges are

connected to the 1

, 4

, 5

, 9

and 10

VNs, in accordance

to the position of the 1s in the top row of H in (13).

The degree of a node is deﬁned as the number of other nodes

that it is connected to and is equal to the corresponding row or

column weight in H. The degree of the CNs D

and the degree

of the VNs D

are important parameters in an LDPC code. If

all CNs have the same degree D

and all VNs have the same

degree D

, the LDPC code is said to be regular. If either value

varies from node to node, the code is said to be irregular and

and D

can be expressed as the average degree over all

nodes. For example, the factor graph of Fig. 4 is irregular with

= 5.75 and D

= 2.3. In any case, the number of 1s in

the PCM H must be the same regardless, whether it is viewed

row-by-row or column-by-column, giving D

×M = D

×N ,

with D

= D

× (1 − R).

C. LDPC decoding

LDPC codes are typically decoded using a belief propa-

gation (BP) algorithm in which messages – typically in the

form of LLRs – are iteratively passed in both directions along

the edges between connected nodes [19]. For example, Fig. 4

illustrates a message ˜q

4−1

sent from the 4

VN v

to the 1

CN c

, while the message ˜r

4−9

is sent from the 4

CN c

to the 9

VN v

. The messages provided as inputs to a node

are processed by activating that node, causing it to create new

output messages that are sent back to the nodes it is connected

to. Thus the processing of the LDPC decoder is delegated to

the many individual calculations performed by the individual

nodes, rather than being a single monolithic global equation.

An important facet of the belief propagation algorithm is that

any message sent to a particular node does not depend on

the message received from that node. For example, CN c

is connected to VNs v

, v

and v

; however, the

message ˜r

2−5

it sends to v

will be calculated based only

on the messages it has received from v

, v

and v

Nodes are activated in an order determined by the LDPC de-

coder’s schedule. This has a signiﬁcant effect upon the LDPC

decoder’s error correction capability, as well as on its other

characteristics. Many different schedules exist and the most

common options will be outlined in Section II-C1. Following

this, variations of the speciﬁc calculations performed within

CNs and VNs will be presented in Sections II-C2 and II-C3

respectively.

1) Scheduling: The schedule of the LDPC decoding pro-

cess determines the order in which VNs and CNs are pro-

cessed, as well as whether multiple nodes are processed in

parallel. Many scheduling variations exist, but the three most

common schedules are described here, namely ﬂooding [20],

Layered Belief Propagation (LBP) [21] and Informed Dynamic

Scheduling (IDS) [22].

Flooding is perhaps the most conceptually simple LDPC

decoding schedule. Here, the factor graph is processed in an

iterative manner, where each iteration comprises the simul-

taneous activation of all CNs, followed by the simultaneous

activation of all VNs [19]. An example of this schedule is

depicted in Fig. 5. It can be seen that at ﬁrst the CNs c

–c

shown in dark grey calculate their messages, which are then

Fig. 5. An example of the ﬂooding schedule

IEEE COMMUNICATIONS SURVEYS AND TUTORIALS 6

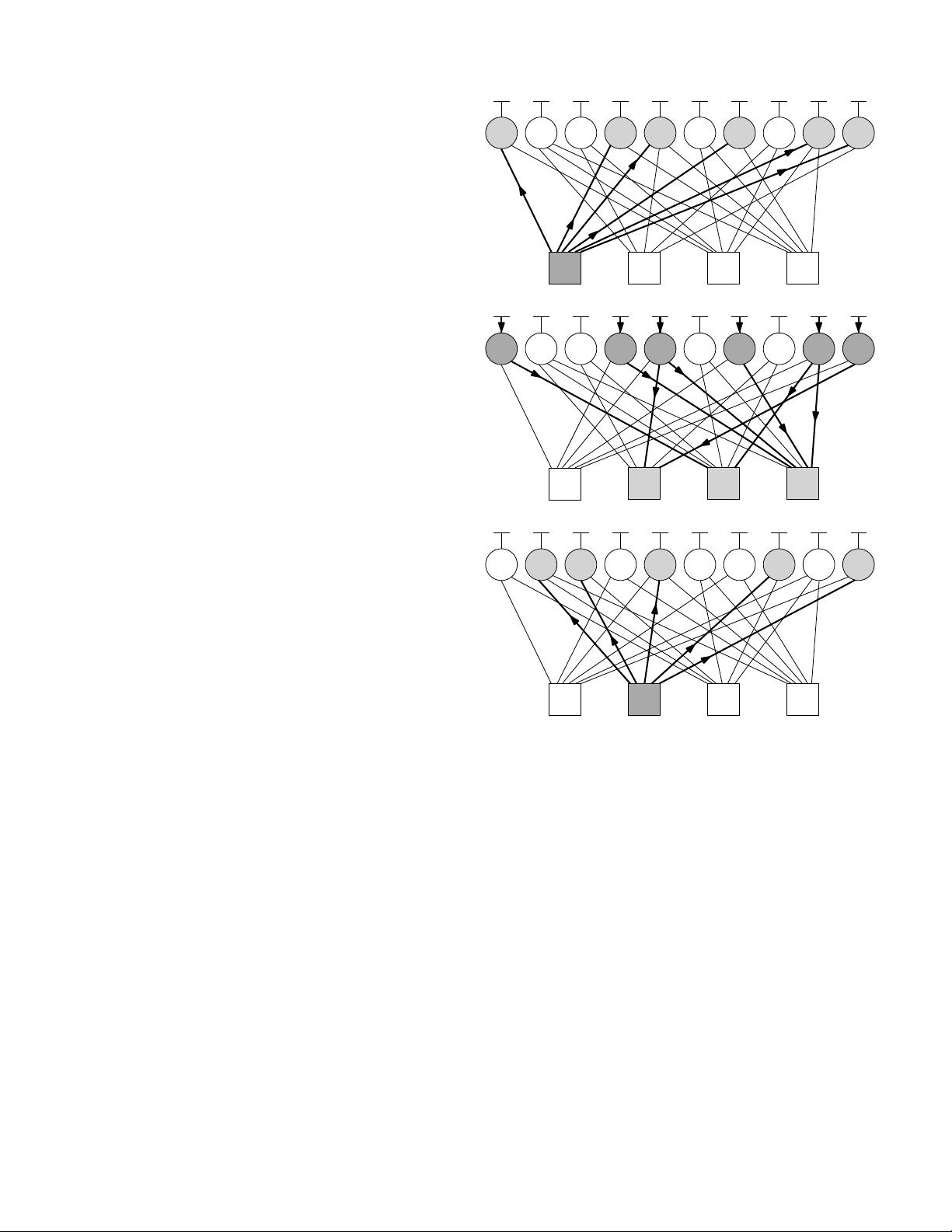
sent along every edge (in bold) to every receiving VN, shown

in light grey. In the second half-iteration, the VNs are shown

in dark grey to indicate that they are performing calculations,

while the CNs are only receiving messages, so they are shown

in light grey.

While Layered Belief Propagation also operates in an

iterative manner, it processes the nodes more sequentially

within each iteration, activating only one or a speciﬁc subset

of nodes at a time [21]. LBP is commonly operated in a CN-

centric manner, processing each CN in turn. Once a CN has

been activated, all of its connected VNs are activated before

moving on to the next CN. Once every CN has been processed,

the iteration is complete. Using Fig. 6 as an example, LBP

may commence each decoding iteration by activating CN c

ﬁrst, sending messages to each of its connected VNs: v

, v

and v

. Each of these VNs may then be activated,

sending new messages to each of their connected CNs, except

. Following this, c

may be activated, allowing it to make

use of the new information received from v

and v

alongside

the information previously received from its other connected

VNs. This process continues until every CN has been activated,

which then marks the end of one decoding iteration.

LBP has the advantage that the information obtained during

an iteration is available to aid the remainder of the iteration.

Owing to this however, it does not have the same high level

of parallelism as the ﬂooding schedule, possibly resulting in a

lower processing throughput and a higher processing latency.

It can also be seen that M CN activations and D

× M VN

activations occur per iteration, resulting in a higher computa-

tional complexity per iteration, when compared to the ﬂooding

schedule. However, it will also be shown in Section II-C2

that CN activations can be signiﬁcantly more computationally

expensive than the VN activations, hence the increased cost

is manageable. Additionally, LBP tends to converge to the

correct codeword using fewer iterations and therefore with

lower computational complexity than ﬂooding [17], resulting

in lower complexity overall.

Informed Dynamic Scheduling inspects the messages that

are passed between the various nodes, selecting to activate

whichever node is expected to offer the greatest improvement

in belief [22]. This requires IDS to perform additional calcula-

tions in order to determine which node to activate at each stage

of the decoding process. However, IDS facilitates convergence

using fewer node activations than in either ﬂooding or LBP,

which may lead to a lower complexity overall.

During IDS, the difference between the previous message

sent over an edge and the message that is obtained using

recently-updated information [23] is calculated. This differ-

ence is termed the residual, and represents the improvement

in belief that is achieved by the new message. Like the LBP

schedule, IDS is commonly centred on the CNs. At the start

of the iterative decoding process, the residual for each output

of each CN is calculated as the magnitude of the message to

be sent over that edge. The message with the greatest residual

is identiﬁed, and the receiving VN is then activated, sending

updated messages to each of its connected CNs. These CNs

then calculate new residuals for each of their edges as the

difference between its new message and its previous message.

Fig. 6. An example of the layered belief propagation schedule

All of the residuals in the graph are then compared for the

sake of identifying the new maximum, before the process is

repeated.

Using Fig. 7 as before, suppose that at the start of the

iterative decoding process, the message ˜r

3−8

from CN c

identiﬁed as having the highest magnitude of all the check-to-

variable messages in the graph. Owing to this, ˜r

3−8

is passed

to the VN v

, which is then activated, in order to obtain

the message ˜q

8−2

which is then passed to c

. The CN c

can then be activated to calculate new residuals for its other

four edges, as the difference between their previous messages

and their new messages that have been obtained using the

updated information from v

. These new residuals are then

compared with the others from the previous step, allowing a

new global maximum to be identiﬁed, to inform the next step

of the decoding process. Note that the next highest residual

within the factor graph does not necessarily have to originate

from the most recently updated CN c

. In the example seen in

Fig. 7, it can be seen that c

is activated to calculate residuals

but it is ˜r

1−4

from CN c

to VN v

that is sent. This implies

剩余25页未读，继续阅读

斩月904

粉丝: 77
资源: 5

FPGA上的LDPC解码器：一项综合调查

LDPC.rar_C-MEX ldpc_LDPC matrix_LDPC regular_LDPC regular AWGN_m

Structural Analysis of Array-Based Non-Binary LDPC Codes

Construction of High-Performance Array-Based Non-Binary LDPC Codes With Moderate Rates

EXIT-Chart-Based LDPC Code Design for 2D ISI Channels

ldpcmatlab代码-Simple-platform-to-Study-5G-LDPC-codes-and-decoders:研究5GeM

matlab代码影响-Upper-bound-on-code-distance-of-QC-LDPC-codes-based-on-MacKa

Construction of Rate-Compatible LDPC Codes

EMS-decoder-of-NB-LDPC-codes:NB-LDPC码的扩展最小和解码器。 使用截短的低值LLR降低MS的复杂度

将DVB-S2 LDPC 64800码缩短为8100：该程序可以生成长度为8100的短码DVB-S2 LDPC 64800的奇偶校验矩阵。-matlab开发

Parity-check--matrix--construct-of-Gallager-LDPC-_QUE SERA_matri

最新资源

EMS-decoder-of-NB-LDPC-codes:NB-LDPC码的扩展最小和解码器。使用截短的低值LLR降低MS的复杂度