汉诺塔问题与递归算法解析

"C++长训基础@递归——拓展.pdf" 在C++编程中，递归是一种强大的技术，常用于解决复杂的问题。递归函数是自身调用自身的函数，它通常涉及分治策略，将大问题分解为相同或相似的小问题来解决。递归在汉诺塔问题中得到了很好的体现，这是一个经典的计算机科学问题，同时也是理解和学习递归的好例子。 汉诺塔问题源自印度古老的传说，其核心是将一叠大小不一的圆盘从一根柱子（源柱）移动到另一根柱子（目标柱），中间可以用第三根柱子（过渡柱）作为辅助，但每次只能移动一个圆盘，并且大盘子不能放在小盘子上方。问题的关键在于找到最小步骤的移动方案。 递归解决汉诺塔问题的算法思路如下： 1. 基本情况：如果圆盘数量只有1，那么直接将该圆盘从源柱移动到目标柱，结束递归。 2. 递归步骤：对于n个圆盘，首先将n-1个圆盘从源柱移动到过渡柱，然后将第n个圆盘从源柱移动到目标柱，最后再将那n-1个圆盘从过渡柱移动到目标柱。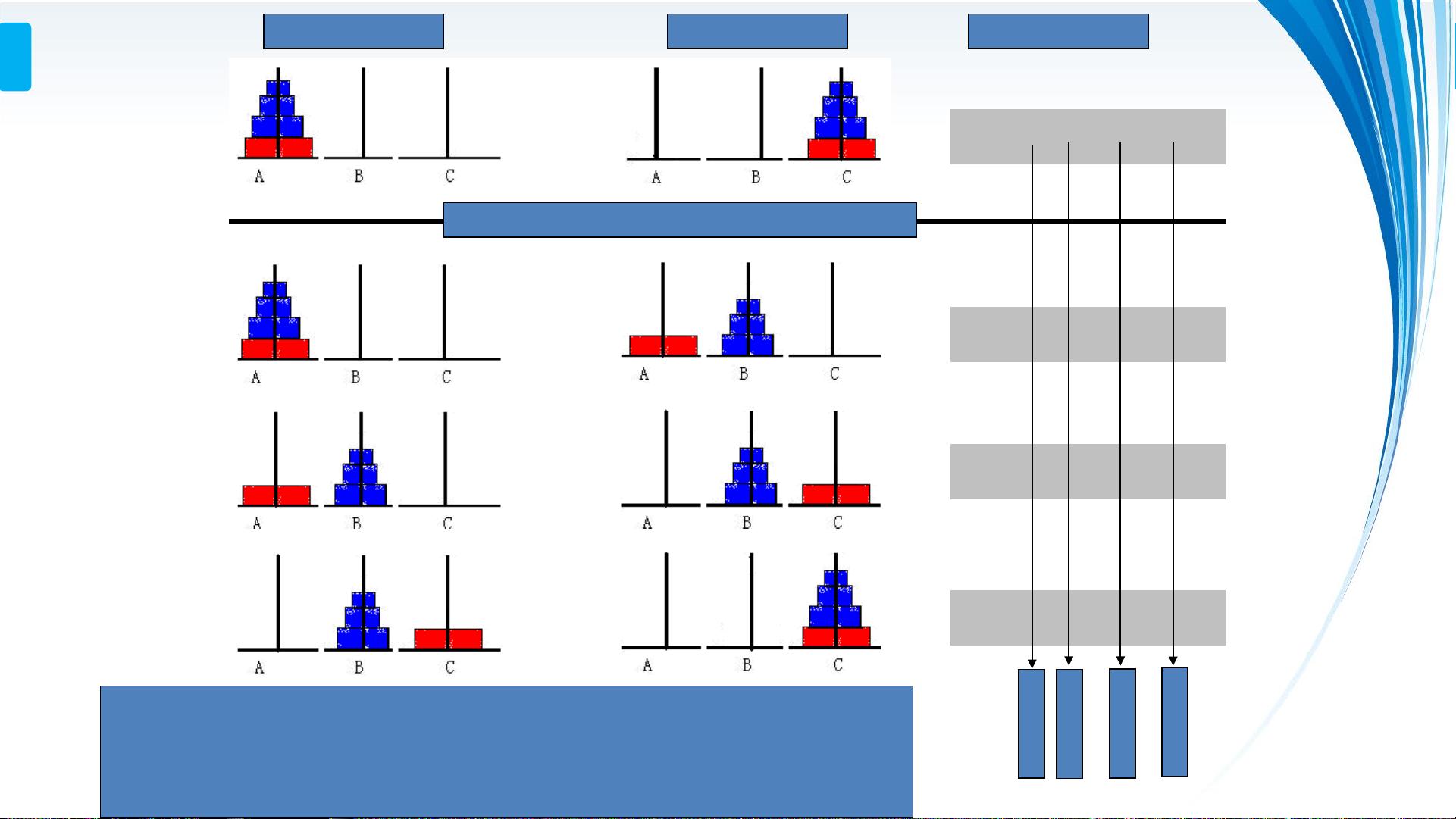 以3阶汉诺塔为例，其移动顺序为：A→C，A→B，C→B，A→C，B→A，B→C，A→C。这里的A、B、C分别代表三根柱子，A是源柱，C是目标柱，B是过渡柱。 在实现递归解决方案时，我们需要定义一个递归函数，如`Hn`，接受三个参数：圆盘数n、源柱、目标柱和过渡柱。对于输入示例`3`，输出示例展示了每个步骤的移动，包括将3个盘子从A移到C的过程，通过B柱作为过渡。 递归函数的定义大致如下： ```cpp void Hn(int n, char from, char aux, char to) { if (n == 1) { // 基本情况：单个盘子直接移动 cout << from << "To" << to << endl; } else { // 递归步骤 Hn(n - 1, from, to, aux); // 将n-1个盘子从from移动到aux cout << from << "To" << to << endl; // 将第n个盘子从from移动到to Hn(n - 1, aux, from, to); // 将n-1个盘子从aux移动到to } } ``` 通过递归，我们可以将一个看似复杂的任务分解为一系列简单的操作，使得问题变得容易处理。在C++编程中，理解和掌握递归概念对于解决复杂问题至关重要，尤其是在数据结构（如树和图）和算法（如排序和搜索）中。递归不仅提高了代码的可读性，也往往能带来高效的解决方案。