图与网络优化：最小支撑树原理

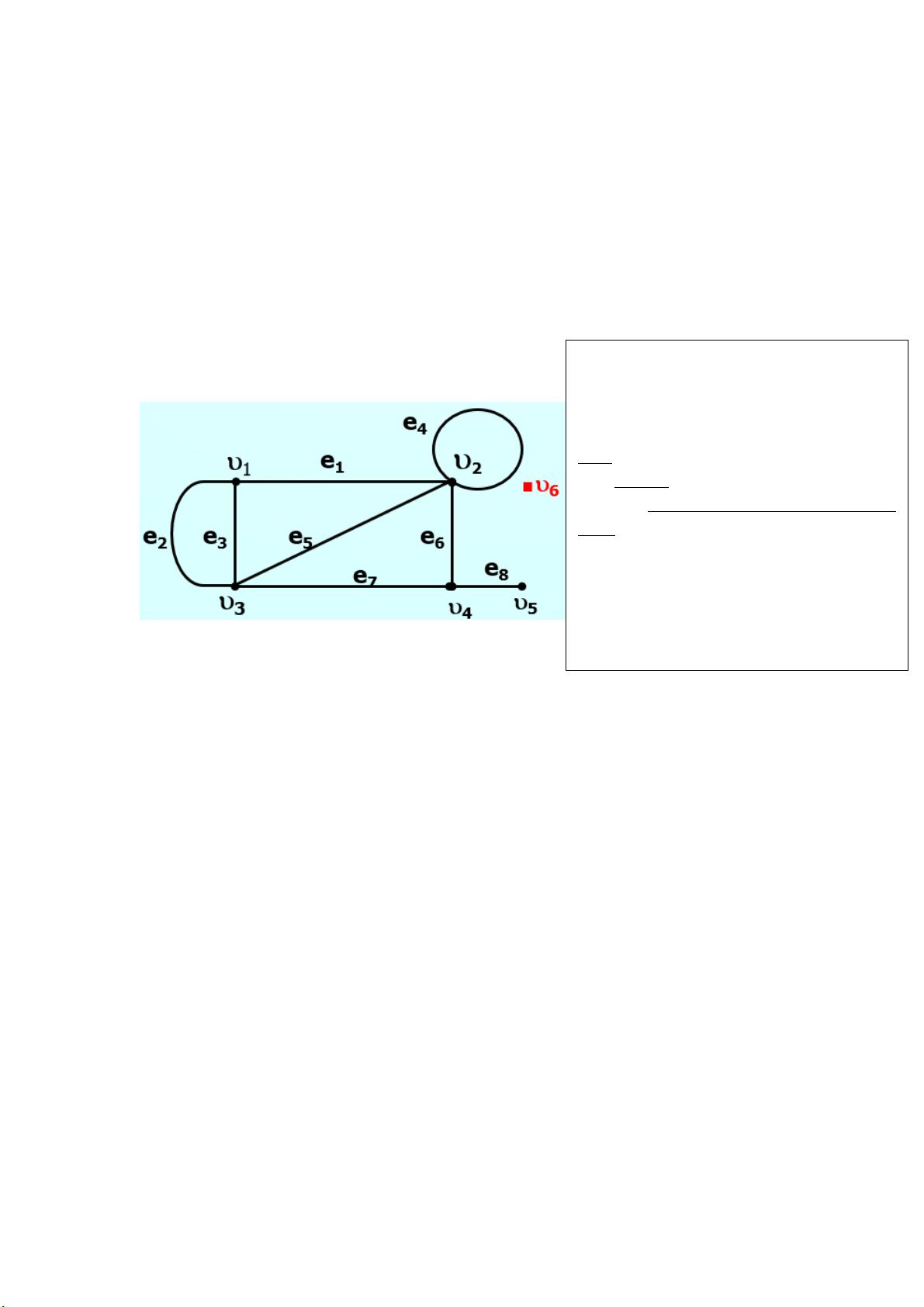
"网络规划之最小支撑树1" 在IT领域，网络规划是至关重要的，尤其是在涉及图与网络优化的问题时。这个问题广泛应用于各种工程和管理情境，利用线性规划和其他算法来解决具有图结构的问题。图与网络优化的独特之处在于它的直观性和简捷性，与传统的单纯形算法相比，其优化算法更易于理解和实施。 首先，我们要理解图的基本概念。图被定义为一个由顶点（又称节点或点）和边组成的集合，记为𝐺=(𝑉,𝐸)，其中𝑉是顶点集，𝐸是边集。边可以是无方向的，也可以是有方向的，这取决于问题的特性。例如，在无向图中，边\(𝑒_{𝑗𝑡}=(𝑣_{𝑖𝑡−1},𝑣_{𝑖𝑡})\)连接两个不同的顶点，而有向图中，弧\(𝑎_{𝑗𝑡}=(𝑣_{𝑖𝑡−1},𝑣_{𝑖𝑡})\)指定了从一个顶点到另一个顶点的方向。 图的类型多种多样，包括简单链（所有边都不同）、初等链（所有顶点都不同）、圈（至少有三个不同顶点的闭链）。连通图是任何两个顶点之间至少存在一条路径的图，反之则为不连通图。此外，图还可以进一步分为环、多重边和简单图，其中简单图不包含环且没有重复的边。 在图中，端点是指边的连接点，关联边是指与同一顶点相关的边。顶点的次（或度）表示与该顶点相邻的边的数量。奇点是度为奇数的顶点，而偶点则是度为偶数的顶点。孤立点则是与任何边都不相邻的顶点。 两个重要的定理在图论中扮演着核心角色： 1. 度数定理：图𝐺=(𝑉,𝐸)中所有顶点的度数之和是边数的两倍，即\(\sum_{𝑣\in𝑉}𝑑(𝑣)=2𝑞\)，其中𝑞是边的数量。 2. 奇偶点定理：在任意图中，奇点的总数等于偶点的总数，即\(\sum_{𝑣\in𝑉_1}𝑑(𝑣)+\sum_{𝑣\in𝑉_2}𝑑(𝑣)=\sum_{𝑣\in𝑉}𝑑(𝑣)\)，其中𝑉_1是奇点的集合，𝑉_2是偶点的集合。 最小支撑树问题是在赋权图中寻找一棵树，这棵树包含图中的所有顶点，并且树的所有边的权重之和尽可能小。这个问题在网络规划中非常关键，特别是在设计通信网络、交通网络等时，以确保成本效益。 在C#这样的编程语言中，解决这些问题通常涉及数据结构如图的实现，以及搜索算法如深度优先搜索或广度优先搜索来找到最小支撑树。例如，Kruskal's算法或Prim's算法常用于求解最小生成树问题，它们分别通过选择最小权重的边并避免形成环路，或者逐步增加连接当前树与新顶点的最小权重边来构建树。 网络规划中的最小支撑树问题涉及到图的基本概念、图的性质、定理以及在实际问题中的应用。理解这些概念对于有效地进行网络设计和优化至关重要。