支持向量机回归教程：算法与应用

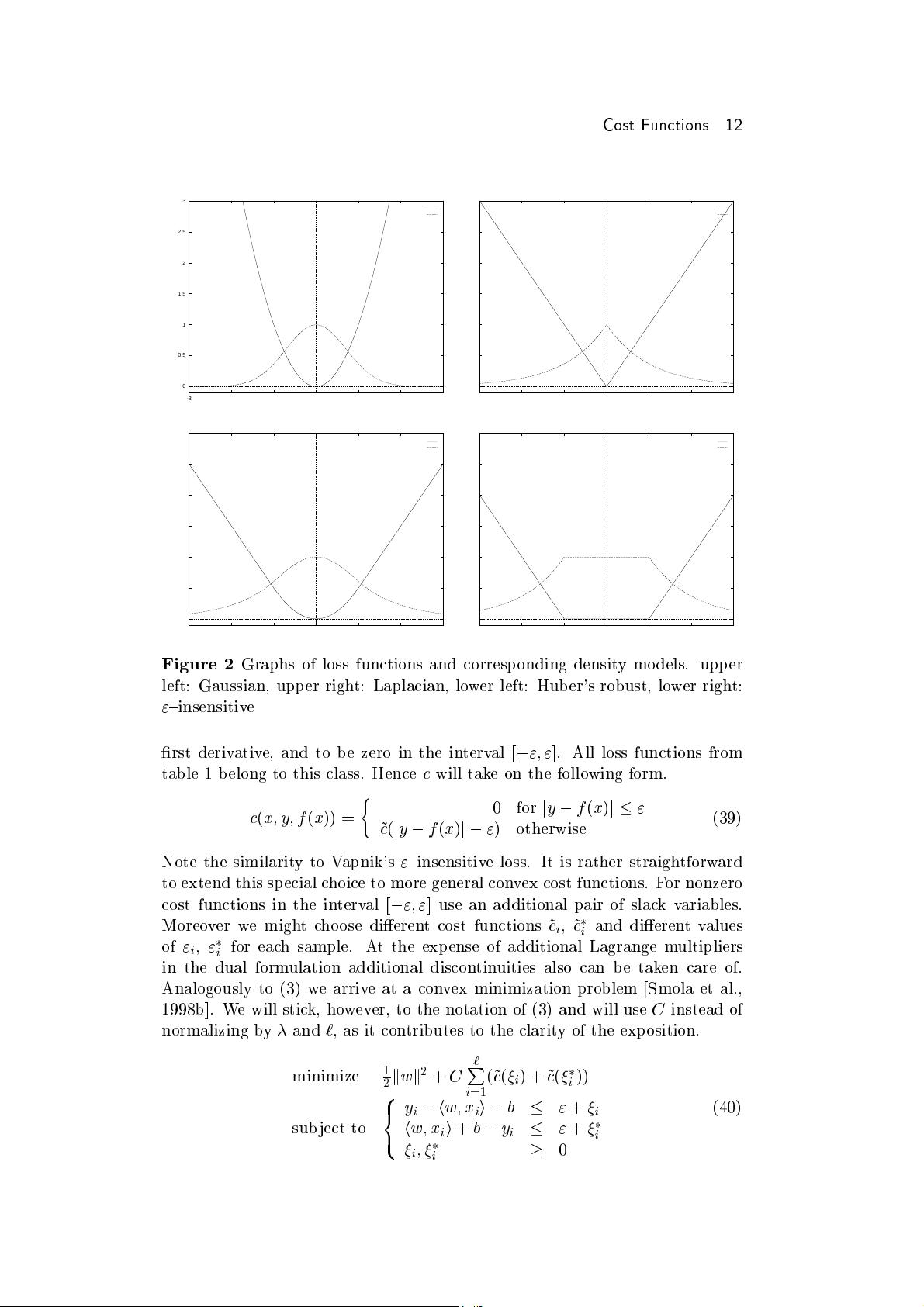
"这篇教程是关于支持向量回归(Support Vector Regression, 简称SVR)的介绍，由Alex J. Smola和Bernhard Scholkopf撰写，属于GMD NeuroCOLT技术报告系列。文章涵盖了SVR的基本概念、训练算法以及处理大规模数据集的高级方法，并提到了一些对SVR的改进和扩展。" 支持向量机（Support Vector Machines, SVM）最初是作为分类工具被提出的，但后来发展出支持向量回归（Support Vector Regression, SVR）以应对连续变量预测问题。在SVR中，模型的目标是找到一个能够最小化预测值与真实值之间误差的超平面。这个超平面通过最大化与最近的数据点（称为支持向量）的距离来确定，从而确保模型具有良好的泛化能力。 本文首先介绍了SVR的基本思想：通过构造一个间隔最大化的边界来拟合数据，这个边界可以容忍一定程度的误差，即ε-范数损失函数。ε-范数允许在模型预测值与实际值之间存在一定的差距（ε-tube），只要大部分数据点在这个范围内，模型就被认为是有效的。 接着，教程详细讲解了训练SVR的算法。最常用的是基于凸优化问题的Quadratic Programming（QP）求解器，这包括解决线性可分情况下的硬间隔最大化和非线性情况下的软间隔最大化。对于非线性问题，SVM通常采用核技巧，如高斯核（RBF）、多项式核或Sigmoid核，将数据映射到高维空间，使得原本在原始空间中难以分离的数据在新空间中变得容易处理。 对于大规模数据集，传统的QP方法可能会面临计算复杂性和内存限制。因此，文章提到了一些高效算法，如Sequential Minimal Optimization (SMO) 和 Cutting Plane Methods，它们能够在训练过程中有效地处理大量数据，同时保持较好的性能。 最后，作者讨论了对SVR的一些修改和扩展，例如引入惩罚项以控制模型复杂度，防止过拟合；或者使用在线学习算法进行增量训练，适应动态数据流。此外，他们还可能涉及了多任务学习、异常检测等应用场景，以及如何结合其他机器学习方法提升SVR的性能。 这篇教程对于理解支持向量回归的核心原理及其在实际应用中的优化策略具有很高的参考价值，适合对机器学习和统计建模感兴趣的读者深入学习。