贪心算法详解与Prim、Kruskal算法应用

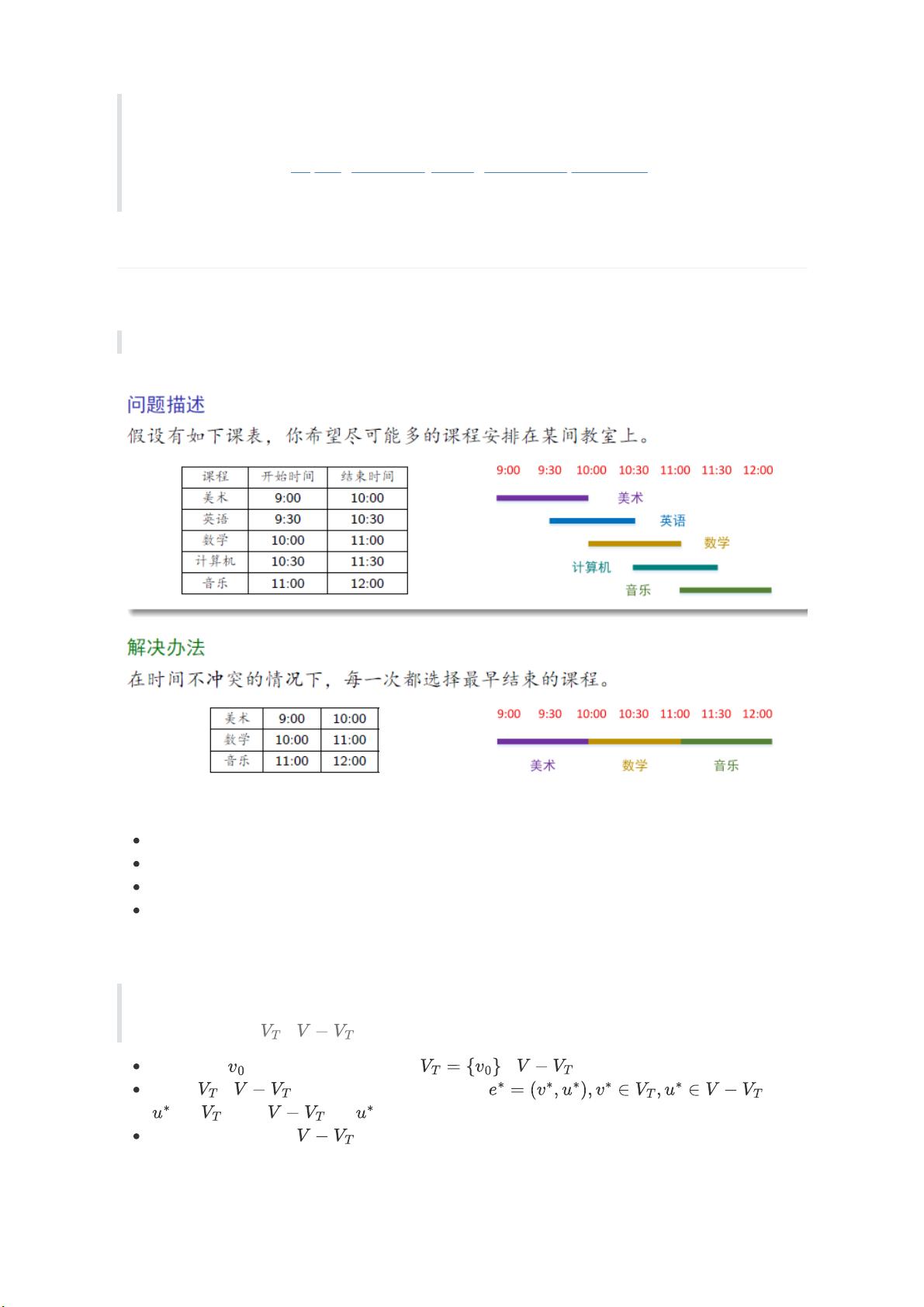
"贪心算法是计算机科学中解决问题的一种策略，它通过在每一步选择局部最优解来尝试达到全局最优解。贪心算法并不总是能找出问题的最优解，但在某些特定情况下，如教室调度问题，它能够有效地找到解决方案。在教室调度问题中，选择最早结束的课程可以确保找到一个有效的安排，而选择最小占用时间或最早开始的课程则可能无法得到最优解。 贪心算法的一个经典应用是在图论中的最小生成树问题，例如Prim算法和Kruskal算法。最小生成树是一棵树形结构，包含了图中的所有顶点，且其所有边的权重之和最小。Prim算法的核心思想是从一个初始顶点开始，每次选择连接两个顶点集合之间权重最小的边，逐步构建生成树，直到所有顶点都被包含。而Kruskal算法则是先对边按权重非递减顺序排序，然后依次尝试将边加入当前无环的子图中，避免形成环路，直至构建出含有n-1条边的最小生成树。 在Prim算法的实现中，首先标记初始节点为已访问，并将其他所有顶点放入候选集合。接着，在已访问节点和候选节点之间的边中寻找权重最小的边，将其加入树中并移除对应的候选节点。这个过程不断重复，直到候选集合为空，即所有顶点都被包含在生成树中。 Kruskal算法则是在排序后的边列表中，逐条检查边是否加入当前子图会导致环路。如果不会，就将这条边加入子图；如果会，则跳过此边。这个过程持续进行，直到子图中有n-1条边，即形成了一棵最小生成树。 在实际编程中，可能会用到比较函数如`cmp(key1, key2)`来对边进行排序，以便于按照权重进行处理。`cmp`函数返回一个元组，根据元组中的元素大小关系确定边的顺序。 总结来说，贪心算法是一种在每一步都追求局部最优的策略，虽然不保证总能得到全局最优解，但在特定问题如教室调度和最小生成树构建中，贪心算法可以提供高效的解决方案。Prim和Kruskal算法是两种常见的贪心算法实现，分别从不同的角度构建最小生成树。