数据结构课程设计：N皇后与八皇后问题解析

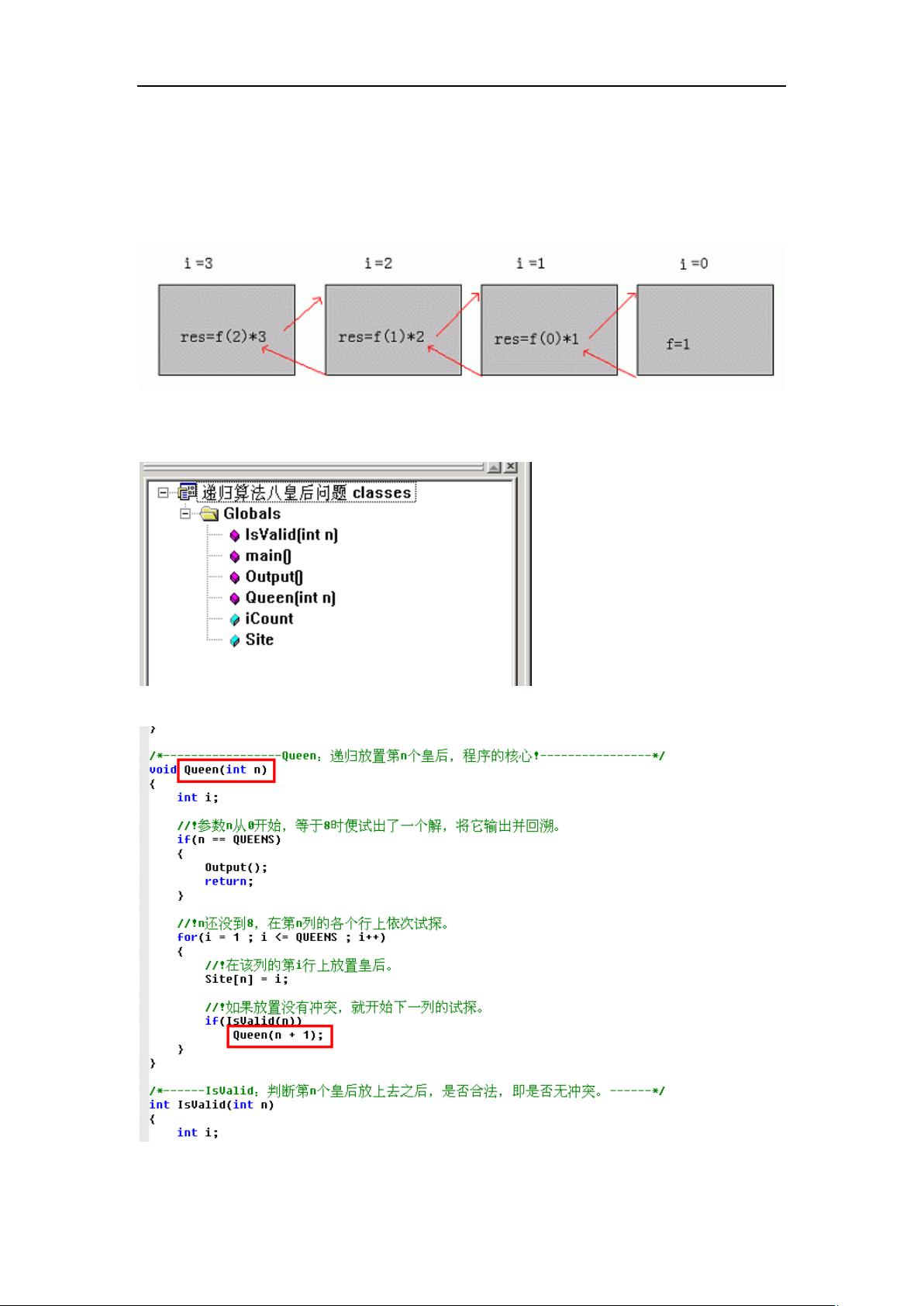
"数据结构课程设计N皇后八皇后" 这篇课程设计报告主要关注的是N皇后问题，特别是其中的八皇后问题。N皇后问题是一个经典的计算机科学问题，它涉及到如何在N×N的棋盘上放置N个皇后，使得没有任何两个皇后能够互相攻击，即任意两个皇后都不在同一行、同一列或同一对角线上。八皇后问题则是N皇后问题的一个特例，因为棋盘的大小固定为8×8。 设计目的是让学生深入理解数据结构和算法的应用，通过解决实际问题来提高问题解决能力和编程技巧。课程设计的基本要求可能包括理解问题的定义、设计合适的算法、实现代码并进行性能分析。 课程设计内容和安排可能涵盖以下部分：首先，介绍八皇后问题的背景知识，包括问题的起源、其在计算机科学中的重要性以及它与数据结构的关联。然后，详细探讨三种不同的解决方案：递归方法、回溯法和堆栈法。 递归方法是解决问题的一种常见策略，它通过将大问题分解为小问题来求解。在八皇后问题中，递归方法会尝试在每个位置放置皇后，并检查是否冲突，如果冲突则回溯到上一步，寻找其他可能的放置位置。报告中提供了递归算法的代码、流程图和运行结果分析，帮助学生理解其实现过程和效果。 回溯法是一种试探性的解决问题的方法，当发现当前路径无法到达目标时，会退回一步，尝试其他路径。在八皇后问题中，回溯法通过不断地尝试和撤销放置皇后，直到找到所有可行的解决方案。报告同样给出了回溯法的代码、流程图和运行结果分析。 堆栈法利用了数据结构堆栈的特性，它通常用于解决需要回溯的问题，如深度优先搜索。在八皇后问题中，堆栈可以用来存储每一步的决策，当无法继续放置皇后时，可以从堆栈中回退，尝试其他决策。报告将解释堆栈法的原理，展示使用的函数和变量，以及具体的运行过程。 通过这三种方法的学习和实践，学生不仅能掌握解决八皇后问题的具体策略，还能深入理解递归、回溯和堆栈等核心数据结构和算法概念，提高他们在未来面对类似问题时的解决能力。