Energies 2017, 10, 1115 3 of 15
22
2
2
2
1
0
1
0
[, ] [ ] , 0
1
[,0] [ ], 0
m
imk
N
nN
m
N
m
nmn
SkT X e e n
NT NT
m
SkT X n
NNT
π
π
−
−
=
−
=
+
=≠
==
(2)
where
,(0, 1)kmn N∈−
. N is the sampling number, and T is the sampling interval. X[n/NT] is the
discrete Fourier transform of x[jT], and
22 2
2/mn
e
π
−
is the Fourier spectrum of the Gaussian window
function.
As seen from Equation (2), the S transform result of a discrete signal is a complex matrix. A row
vector of the matrix represents the frequency-magnitude characteristic of the signal at a specific
moment, and the frequency interval is 1/NT, denoted by f0. A column vector represents the
time-magnitude characteristic of a frequency component with a specific frequency, and the time
interval is T. For example, we denote the S transform result by S, and S[k + 1, n + 1] represents the
frequency component with a frequency of nf0 at the time kT.
The wavelet transform provides a cogent math tool for transient signal analysis. However, the
wavelet transform results for a signal may be different under different wavelet bases and scales;
thus, it is imperative to select the proper wavelet basis and scale for a specific signal. The Fourier
transform has a window with a fixed height and width; thus, it cannot adjust the time–frequency
resolution with variations of the time and frequency. The S transform inherits the advantages of the
wavelet transform and the Fourier transform, and can overcome both of their shortcomings. The S
transform is perfectly reversible. The phase of the S transform referenced to the time origin provides
useful and supplementary information regarding spectra that is not available from locally
referenced phase information in the wavelet transform [16]. By means of the S transform, all the
frequency components with a frequency interval of f0 can be extracted, and the proper frequency
components can be selected conveniently. Additionally, the S transform results are more intuitive
than the wavelet transform results, which will be discussed in detail in Subsection 5.7. The height
and width of the Gaussian window can change with a variation of the frequency; thus, the S
transform can adjust its time and frequency resolution ability with respect to the frequency.
In this paper, the S transform was realized by means of matrix laboratory (MATLAB). We take
a series of signals that contained fault data at 0 ms as an example. The frequency components of the
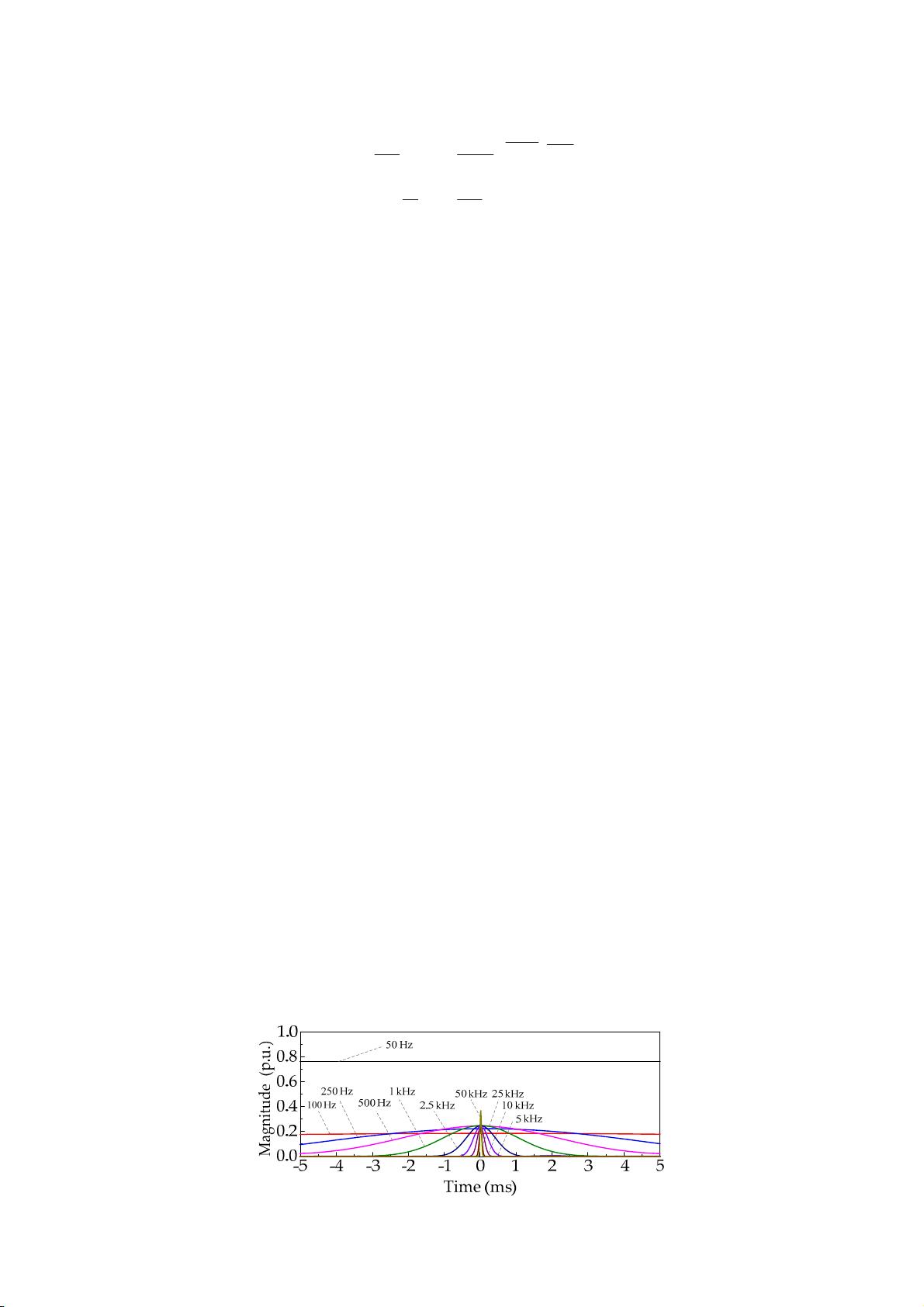
signal were extracted by the S transform, and the time-magnitude curves of some typical frequency
components are shown in Figure 1. As can be seen, when the frequency is lower than 500 Hz, the
time-magnitude curves of the frequency components are smooth, but they are different from each
other. This indicates that, in the low-frequency range, the frequency resolution ability of the S
transform is remarkable, whereas the time resolution ability is not very good. When the frequency
is greater than 2.5 kHz, the time-magnitude curves are concentrated at the fault time; thus, the
transient fault signal can be represented intuitively. This indicates that the time resolution ability of
the S transform is improved in the high-frequency range. For fault identification and location, a
good time resolution ability is more critical. Therefore, due to the satisfactory time resolution ability
of the S transform in the high-frequency range, the high-frequency components were employed for
fault location in this paper.


















