"基于 SAT 的二进制数独游戏求解程序设计与实现"

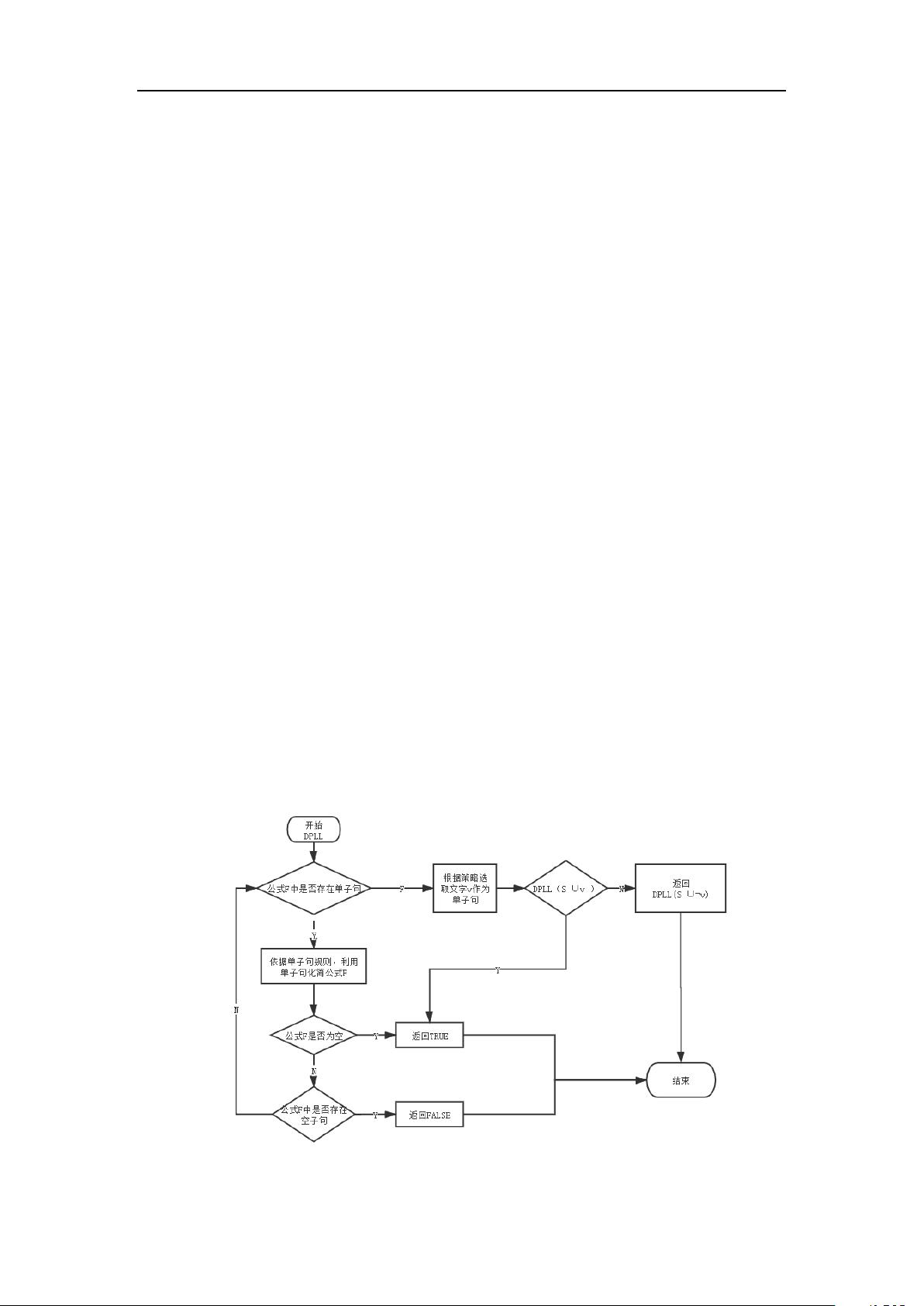
从1960年起，人们一直对SAT问题非常关注，并且世界各国的研究人员在这方面做了大量的工作，提出了许多求解算法。SAT问题指的是命题逻辑公式的可满足性问题，它是计算机科学与人工智能领域的基本问题之一，也是一个典型的NP完全问题。SAT问题在许多实际领域都有着重要的理论意义和应用价值，比如硬件设计和安全协议验证等。 本次课程设计报告的题目是"基于SAT的二进制数独游戏求解程序"，属于计算机科学与技术专业班级为计算机科学与技术1805班。报告的撰写者是于祯奇，指导教师是李丹。报告的日期是2020年3月30日。 该课程设计要求基于DPLL算法实现一个完备的SAT求解器。具体来说，要求对输入的CNF范式算例文件进行解析，并建立其内部表示。在设计求解器时，需要精心设计问题中变元、文字、子句、公式等的有效的物理存储结构，并采用合适的分支变元处理策略，使得求解器能够高效地解决SAT问题。 SAT问题的解决算法之一是DPLL算法。DPLL算法是一种用于解决SAT问题的递归回溯算法，其基本思路是不断地选择未赋值的变元，并通过对其赋值进行推理和验证，来确定整个命题公式的满足性。在本次课程设计中，需要根据DPLL算法的思想，设计一个完备的SAT求解器。 在设计求解器时，首先需要对输入的CNF范式算例文件进行解析。CNF范式是一种常用的表示命题逻辑公式的标准形式，它由多个子句组成，每个子句由多个文字组成，每个文字表示一个变元的取值。解析CNF范式算例文件可以得到其中包含的变元、文字、子句和公式等信息，为后续的求解过程做准备。 接下来，需要设计有效的物理存储结构来表示问题中的变元、文字、子句和公式等。合理的存储结构可以提高求解器的效率和性能。同时，还需要采取一定的分支变元处理策略，根据当前已确定的赋值情况，选择一个未赋值的变元进行赋值，并进行相应的推理和验证。通过不断的回溯和搜索，直到得到整个命题公式的满足性结果。 最终，求解器将输出命题公式的满足性结果，即判断该命题公式是否可满足。如果可满足，则可以得到一个满足该命题公式的赋值。如果不可满足，则说明该命题公式无解。 在完成本次课程设计后，对于SAT问题的理解和求解能力将会有很大的提高。同时，通过参与这样的课程设计，可以提升编程和算法设计的能力，培养解决实际问题的能力。