6 1. INTRODUCTION TO ALGORITHM DESIGN
Several algorithms might come to mind to solve this problem. Perhaps the most
popular idea is the nearest-neighbor heuristic. Starting from some point p
0
, we walk
first to its nearest neighbor p
1
.Fromp
1
, we walk to its nearest unvisited neighbor,
thus excluding only p
0
as a candidate. We now repeat this process until we run
out of unvisited points, after which we return to p
0
to close off the tour. Written
in pseudo-code, the nearest-neighbor heuristic looks like this:
NearestNeighbor(P )
Pick and visit an initial point p
0
from P
p = p
0
i =0
While there are still unvisited points
i = i +1
Select p
i
to be the closest unvisited point to p
i−1
Visit p
i
Return to p
0
from p
n−1
This algorithm has a lot to recommend it. It is simple to understand and imple-
ment. It makes sense to visit nearby points before we visit faraway points to reduce
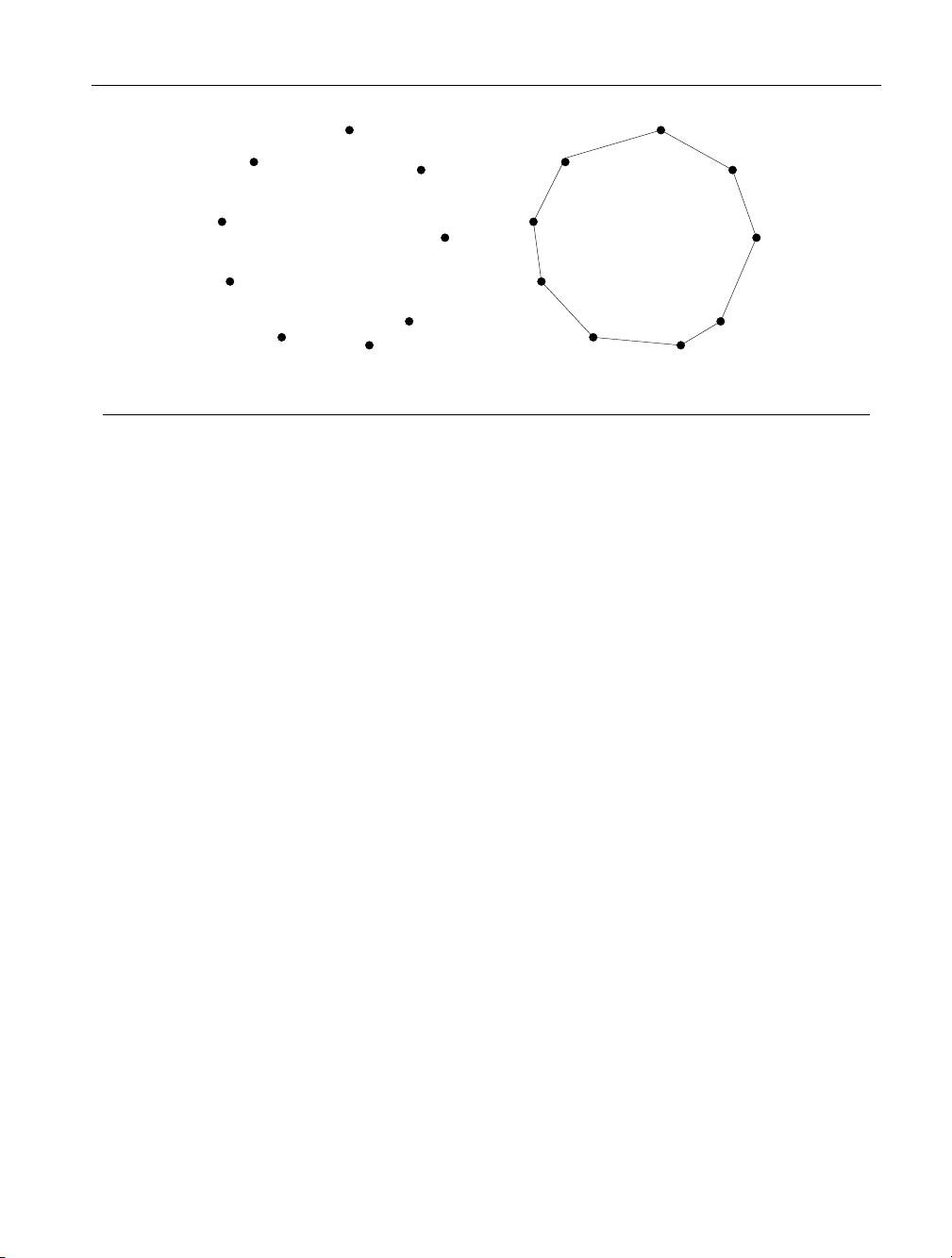
the total travel time. The algorithm works perfectly on the example in Figure 1.2.
The nearest-neighbor rule is reasonably efficient, for it looks at each pair of points
(p
i
,p
j
) at most twice: once when adding p
i
to the tour, the other when adding p
j
.
Against all these positives there is only one problem. This algorithm is completely
wrong.
Wrong? How can it be wrong? The algorithm always finds a tour, but it doesn’t
necessarily find the shortest possible tour. It doesn’t necessarily even come close.
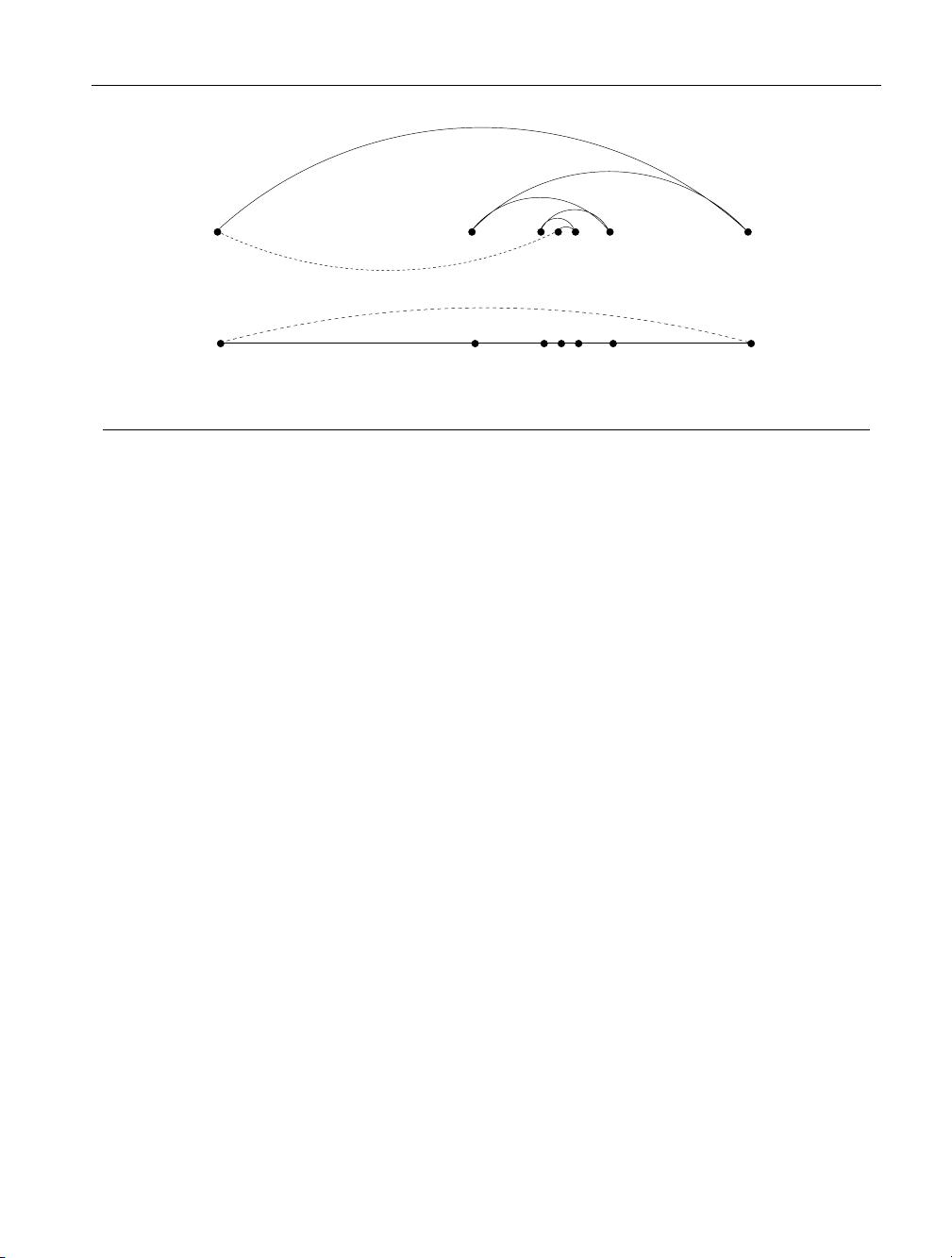
Consider the set of points in Figure 1.3, all of which lie spaced along a line. The
numbers describe the distance that each point lies to the left or right of the point
labeled ‘0’. When we start from the point ‘0’ and repeatedly walk to the nearest
unvisited neighbor, we might keep jumping left-right-left-right over ‘0’ as the algo-
rithm offers no advice on how to break ties. A much better (indeed optimal) tour
for these points starts from the leftmost point and visits each point as we walk
right before returning at the rightmost point.
Try now to imagine your boss’s delight as she watches a demo of your robot
arm hopscotching left-right-left-right during the assembly of such a simple board.
“But wait,” you might be saying. “The problem was in starting at point ‘0’.
Instead, why don’t we start the nearest-neighbor rule using the leftmost point
as the initial point p
0
? By doing this, we will find the optimal solution on this
instance.”
That is 100% true, at least until we rotate our example 90 degrees. Now all
points are equally leftmost. If the point ‘0’ were moved just slightly to the left, it
would be picked as the starting point. Now the robot arm will hopscotch up-down-
up-down instead of left-right-left-right, but the travel time will be just as bad as
before. No matter what you do to pick the first point, the nearest-neighbor rule is
doomed to work incorrectly on certain point sets.