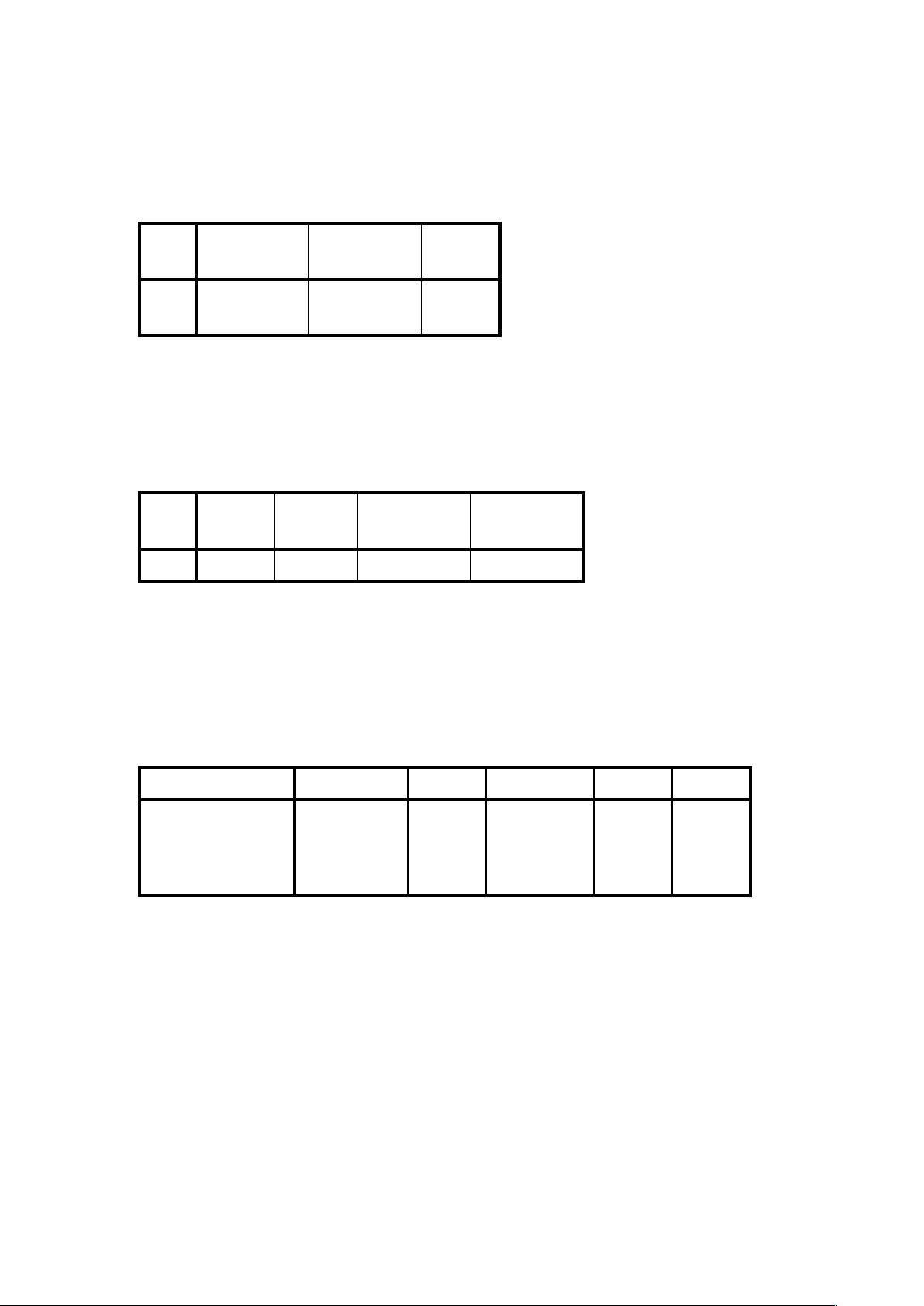
合成纤维强度与拉伸倍数的线性关系分析

回归分析是一种统计方法，用于研究两个或多个变量之间的关系，其中一个变量（因变量）被视为由其他变量（自变量）的函数来预测。在这个"回归分析及应用实例"中，我们关注的是一个具体的实践案例，即探索合成纤维的强度与其拉伸倍数之间的线性相关性。 首先，我们从实验数据出发，观察了12组数据点，每组数据包含拉伸倍数和对应的强度值。为了确定这两个变量之间是否存在显著的相关性，进行了线性回归分析。在回归模型构建过程中，选择了"Enter"方法，即所有提供的拉伸倍数变量都被直接引入到模型中，形成了一元线性回归模型，其中拉伸倍数作为自变量，强度作为因变量。 回归分析的结果表明，模型1的R值为0.986，这是一个非常高的值，接近于1，显示出强烈的正相关性。判定系数R²（决定系数）为0.972和调整后的R²（0.969）进一步证实了这种显著的线性关联。标准误差S为0.41181，它衡量了回归估计的精度，数值较小，意味着模型拟合的精度较高。 方差分析表提供了更深入的统计检验。统计量F的值为347.273，这个大的F值和极低的相伴概率值（P＜0.001）证明了拉伸倍数对强度的影响具有高度统计学意义，即自变量与因变量之间的关系在统计上是显著的。方差分析还区分了回归平方和（58.894，反映了模型解释的变异程度）、残差平方和（1.696，剩余未被模型解释的变异）以及总平方和（60.590，总变异），这些值揭示了模型的解释能力和剩余误差的大小。 最后，系数表列出了回归方程中的参数估计值，包括未标准化系数（Unstandardized Coefficients）和标准化系数（Standardized Coefficients）。这些系数可以用来解读模型的具体含义，例如，每增加一个单位的拉伸倍数，强度平均会如何变化。此外，t值和Sig.（显著性水平）用来评估系数估计的显著性。 这个回归分析实例展示了如何通过线性回归模型来探究两个变量间的关联，并且得出结论：合成纤维的强度与拉伸倍数之间存在强烈且显著的正相关关系。这一结果对于理解纤维性能的潜在规律以及在实际生产中的优化应用具有重要意义。