直线二级倒立摆控制研究与MATLAB仿真的控制策略优化
30 浏览量
更新于2024-06-24
收藏 1.53MB DOC 举报
本文是一篇针对直线二级倒立摆控制系统进行深入研究的本科毕业设计论文。倒立摆,作为一种经典的非线性动力学系统,因其复杂性而成为测试新型控制策略的理想平台。倒立摆的特点包括多变量、强耦合和动态不稳定性,这使得其控制问题具有挑战性。
论文首先回顾了倒立摆系统控制领域的历史发展和现有研究状况,强调了倒立摆作为测试控制理论有效性的重要载体。作者关注的是直线二级倒立摆,这是一种更高级别的系统,其控制设计需要考虑更高的维度和动态特性。
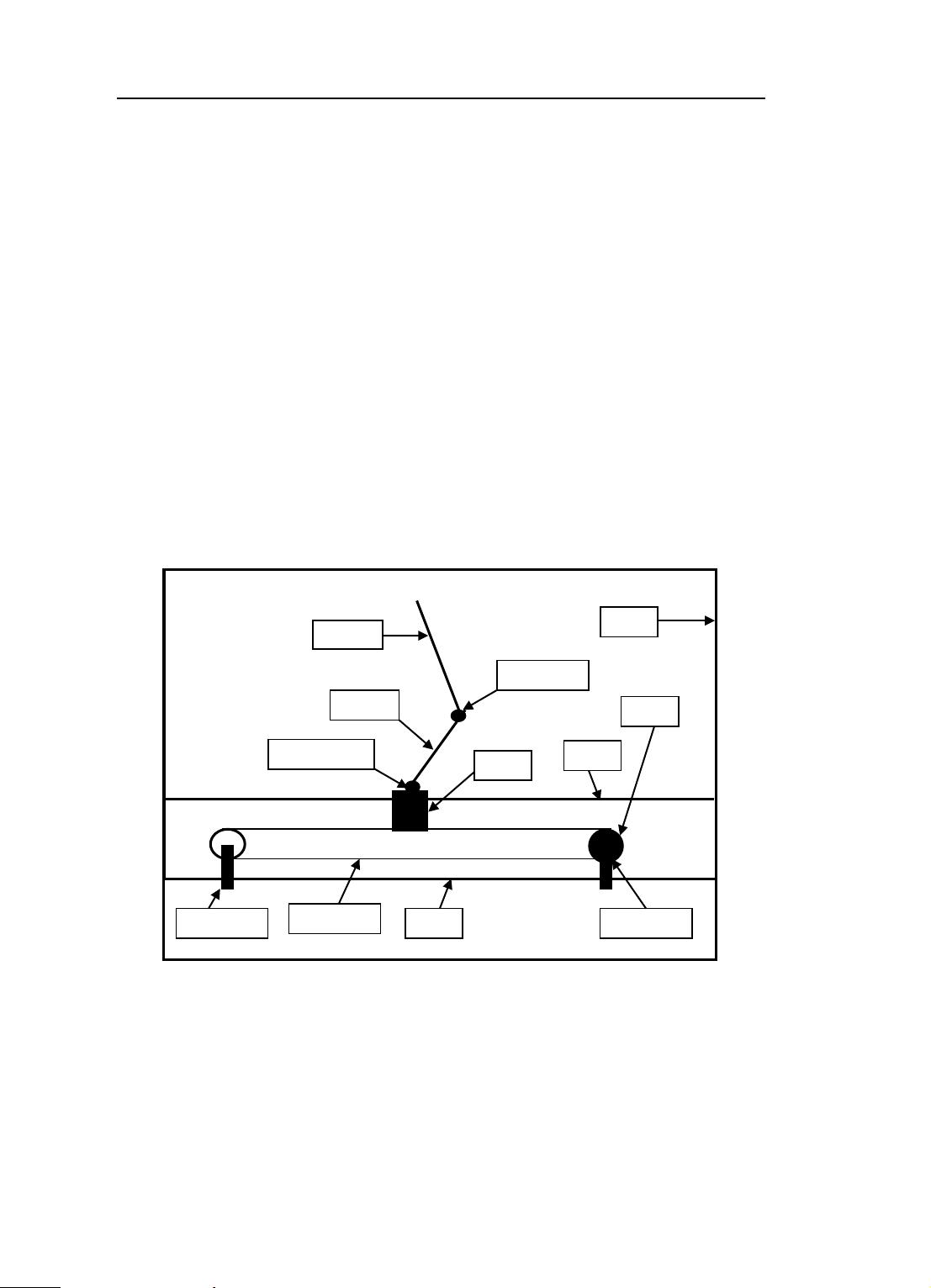
接着,作者详细介绍了直线二级倒立摆的物理结构,并在此基础上推导出了相应的数学模型。这个过程涉及到运动学和动力学分析,可能涉及拉格朗日方程或者传递函数等高级数学工具。通过精确的数学模型,研究者能够理解和预测系统的响应行为,为控制器的设计提供依据。
在控制策略方面,论文采用了两种主要的方法:极点配置和LQR(线性二次鲁棒)最优控制。极点配置是一种直接调整系统动态响应的方法,通过改变系统的特征根位置来改善系统性能。而LQR控制则是通过求解优化问题,找到一个使系统成本函数最小化的控制输入,以实现系统的最佳状态。
作者分别基于这两种方法设计了控制器,并通过MATLAB仿真进行评估。MATLAB作为一个强大的数值计算和仿真软件,被用于模拟实际操作中的控制效果,包括系统响应、稳定性分析和抗干扰能力测试。通过对比分析和仿真结果,论文旨在验证所设计控制器的有效性和优越性,尤其是在应对不确定性和外部干扰时的表现。
总结关键词包括:倒立摆、极点配置、最优控制、MATLAB以及仿真,这些词汇概括了论文的核心内容和研究方法。整篇文章探讨了倒立摆控制问题的解决策略,并通过MATLAB仿真验证其在实际应用中的可行性,对于深入理解非线性系统控制和优化方法具有参考价值。
2023-06-28 上传
2023-07-08 上传
2023-07-05 上传
2021-09-27 上传
116 浏览量
matlab大师
- 粉丝: 2838
最新资源
- ADO数据库编程基础与优势
- Java编程入门:构造函数与自动初始化
- AO学习指南:从入门到精通
- 高速公路养护管理系统需求分析
- 深入解析Java EJB工作原理与RMI面试题
- C#接口详解:实现与应用
- ASP编程入门教程:从基础到实践
- 适应社会:软件测试与个人成长
- 软件测试文档详解:Estudy协同学习系统功能测试关键案例
- C++/C编程最佳实践指南
- Word高效使用技巧:替换文字为图片与便捷操作揭秘
- 语义网的逻辑基础与应用探索
- 测试计划编写全面指南:策略、组织与执行
- 基于C语言的学生信息管理系统设计与实现
- Sun's Java Enterprise Framework (JEF):简化企业级开发
- Linux命令基础与管理操作详解