数据结构:树与二叉树解题指南
需积分: 25 76 浏览量
更新于2024-07-27
收藏 781KB DOC 举报
"数据结构1800题树及二叉树章节答案"
在数据结构的学习中,树和二叉树是重要的概念,它们在计算机科学的许多领域都有广泛应用,如文件系统、编译器设计、数据库索引等。本资料涉及的是关于树和二叉树的1800题解,旨在帮助学习者加深对这部分知识的理解。
1. **栈的运用**
栈是一种线性数据结构,具有后进先出(LIFO)的特点。题目中提到的栈状态访问问题涉及到利用栈的特性进行状态转换分析。例如,在处理递归或表达式求值时,栈常常被用来跟踪函数调用或操作符优先级。
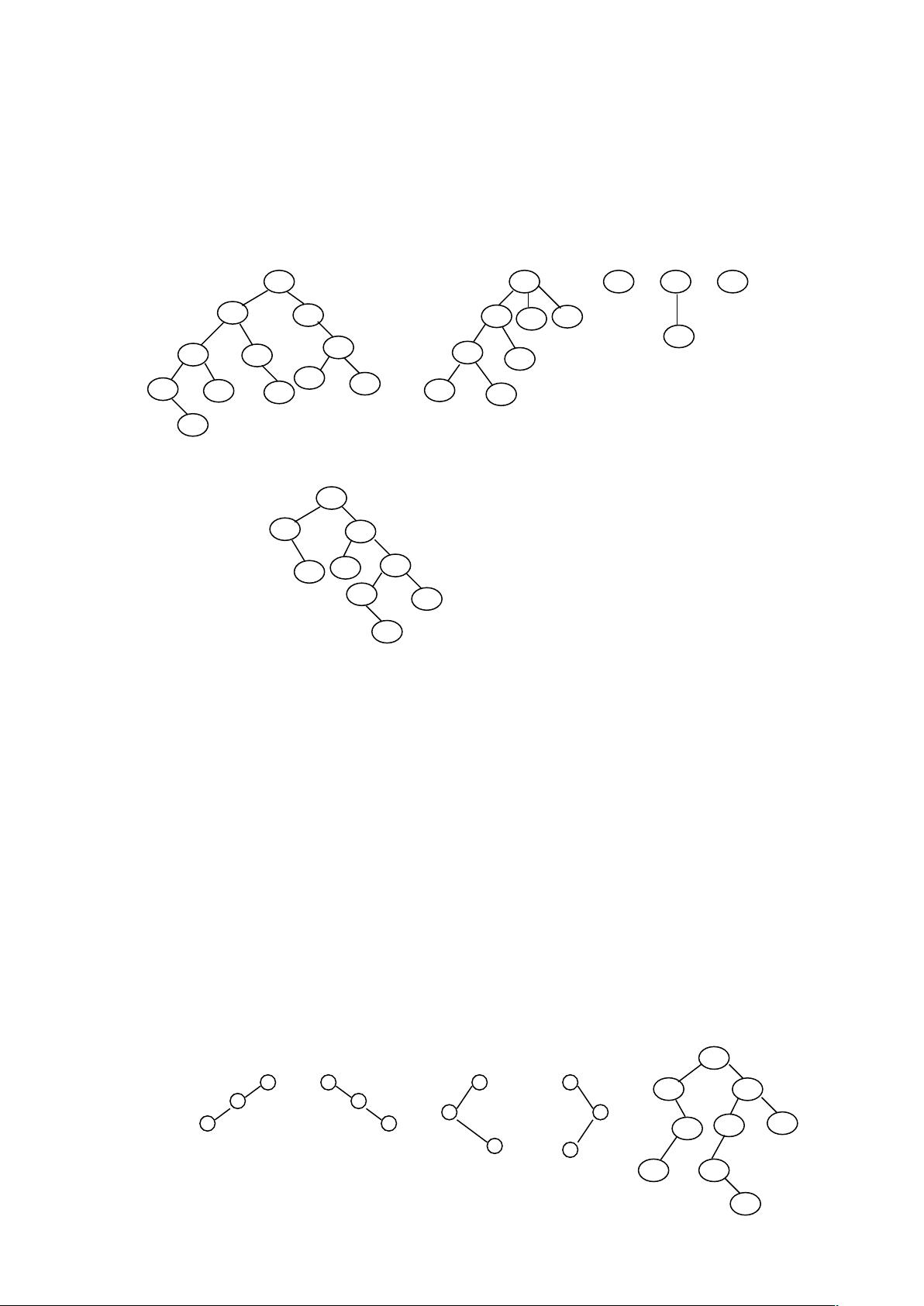
2. **二叉树的遍历**
- 前序遍历:根节点 -> 左子树 -> 右子树
- 中序遍历(对称序):左子树 -> 根节点 -> 右子树
- 后序遍历:左子树 -> 右子树 -> 根节点
这三种遍历方式对于非空二叉树,能分别以不同的顺序访问所有节点。通过遍历序列可以重建二叉树,例如,前序序列和中序序列或者中序序列和后序序列可以唯一确定一棵二叉树,但仅靠前序和后序序列是无法确定的,因为无法区分左右子树。
3. **二叉树的性质**
- 前序序列的第一个元素是根节点,根据中序序列可以将元素分为左右两部分,从而构建左右子树。
- 对于任意二叉树,如果所有叶子节点都在相同相对位置,那么它们在三种遍历序列中都会出现在相同的位置。
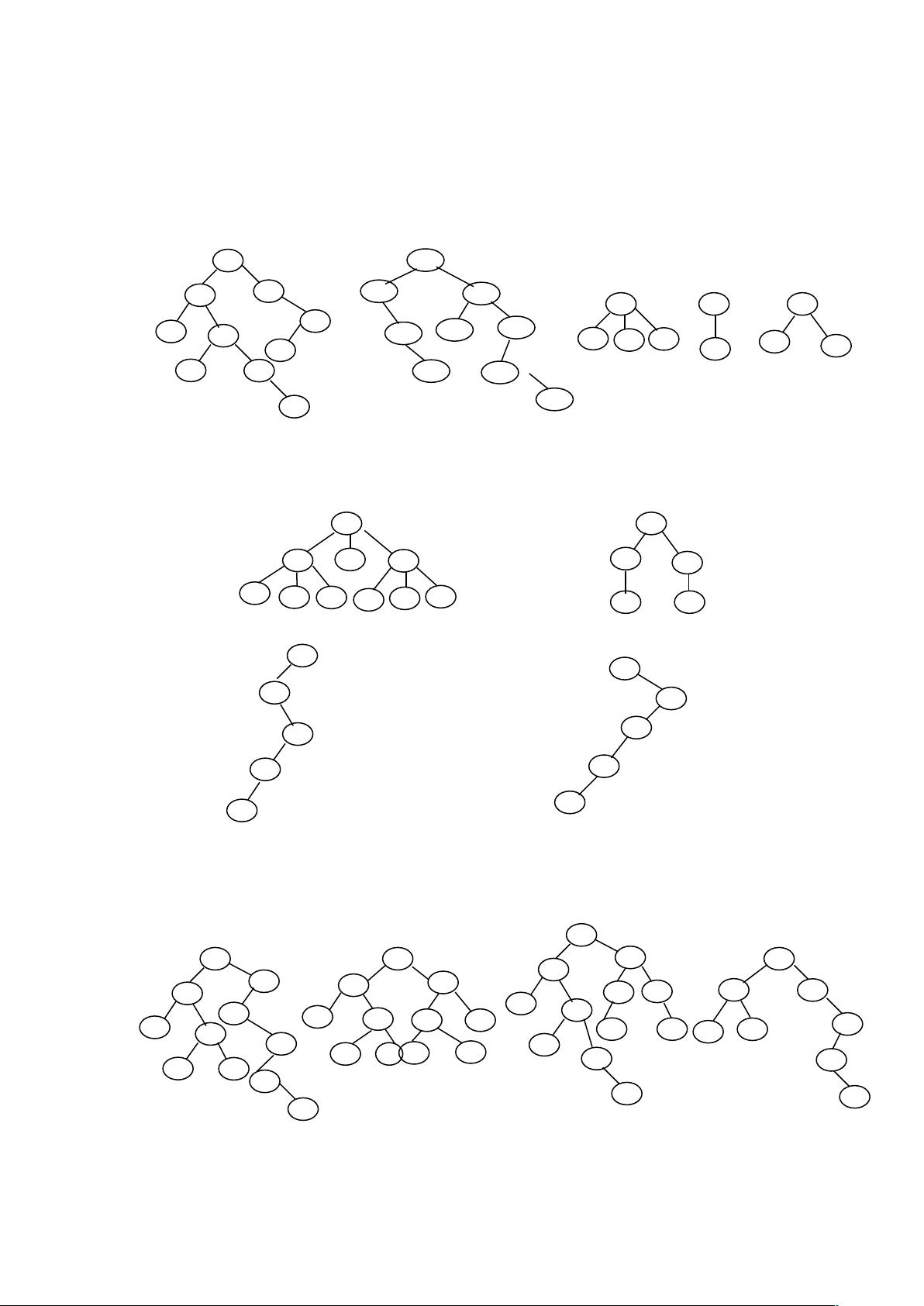
4. **二叉树的构建**
- 当给定一个二叉树的前序和中序序列,可以通过以下步骤构建二叉树:
- 找到中序序列中与前序序列第一个元素相同的节点,这个节点就是根节点。
- 分割中序序列,左边是左子树的中序序列,右边是右子树的中序序列。
- 分别对左右子树序列重复以上步骤,构建子树。
- 类似地,给定中序和后序序列也能构建二叉树:
- 后序序列的最后一个元素是根节点。
- 在中序序列中找到该根节点,分割序列,左边是左子树的中序序列,右边是右子树的中序序列。
- 根据分割后的中序和后序序列构建左右子树。
5. **特殊情况**
- 如果二叉树的所有节点都只有左子树或只有右子树,那么前序和后序序列会相同,但由于没有足够的信息区分左右子树,所以无法唯一确定这棵树。
学习这些知识点对于理解数据结构的基本原理至关重要,同时也为解决实际问题提供了理论基础,比如在算法设计、数据存储和检索等方面。通过解答这些题目,学习者可以深入理解树和二叉树的性质,掌握如何使用遍历序列来构建和分析二叉树。
159 浏览量
点击了解资源详情
1261 浏览量
334 浏览量
136 浏览量
121 浏览量
264 浏览量
166 浏览量
2010-05-19 上传
aaa2496584003
- 粉丝: 0
- 资源: 2
最新资源
- Star UML指导手册
- FAT32文件系统白皮书(中文)
- 领域驱动模型详细介绍
- Asp.net开发必备51种代码(非常实用)
- 智能手机操作系统简介
- 当前,CORBA、DCOM、RMI等RPC中间件技术已广泛应用于各个领域。但是面对规模和复杂度都越来越高的分布式系统,这些技术也显示出其局限性:(1)同步通信:客户发出调用后,必须等待服务对象完成处理并返回结果后才能继续执行;(2)客户和服务对象的生命周期紧密耦合:客户进程和服务对象进程都必须正常运行;如果由于服务对象崩溃或者网络故障导致客户的请求不可达,客户会接收到异常;(3)点对点通信:客户的一次调用只发送给某个单独的目标对象。
- JSP 《标签啊,标签!》
- UDDI 注册中心介绍
- Thinking in C++, Volume 2, 2nd Edition 英文版 (pdf)
- 完全精通局域网.rar
- mtk的make命令分析
- Essential-MATLAB-for-Engineers-and-Scientists-Third-Edition
- Maven 权威指南 简体中文版
- 深入理解计算体系结构英文版
- AT&T汇编学习资料
- 计算机故障查询手册(非高手用)