集合的概念与运算解析

"1.1 集合的概念与运算.pptx" 本文将深入探讨高中数学中的集合理论，这是理解数学基础的重要部分。集合，简单来说，是包含特定对象的总体，这些对象称为集合的元素。集合具有三个基本性质：确定性、互异性以及无序性。这意味着集合内的每个元素都是唯一的，且元素的顺序无关紧要。 1. 集合的含义与表示： 集合的元素必须满足三个特性：确定性（每个元素都有明确的定义）、互异性（不允许重复元素）和无序性（集合不区分元素的排列顺序）。元素与集合的关系通常表示为属于或不属于，用符号"∈"表示属于，"∉"表示不属于。集合的表示方法有列举法（列出所有元素），描述法（通过属性描述元素），以及Venn图法（图形表示）。 2. 集合间的基本关系： - 包含关系：A⊆B 表示A是B的子集，B⊇A表示B包含A。如果A是B的子集但不是B本身，我们写作A⫋B，表示A是B的真子集。 - 等集关系：A=B意味着集合A和B包含完全相同的元素。 3. 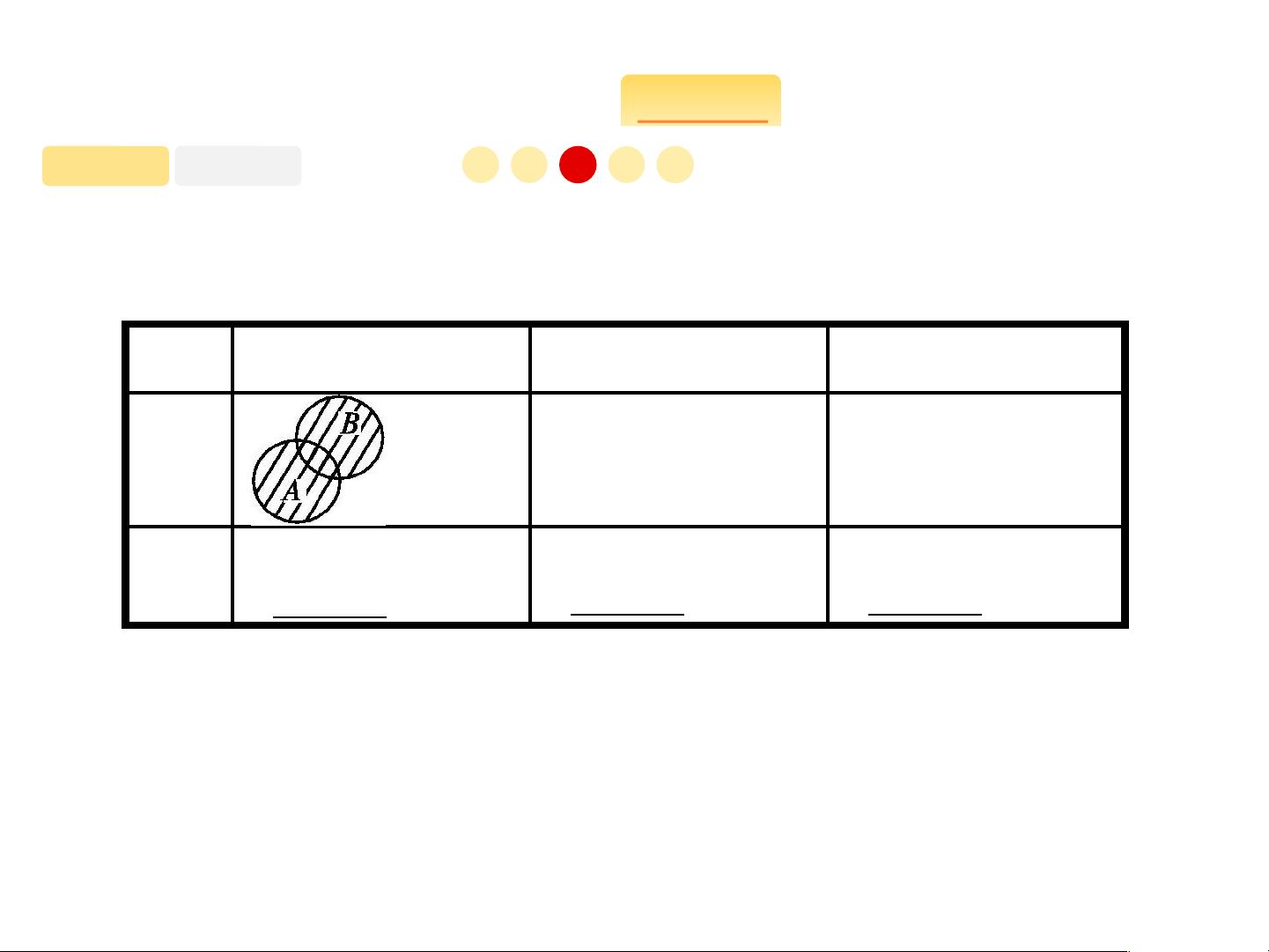集合的运算： - 并集：A∪B表示所有属于A或B的元素组成的集合，表示所有属于A和B的元素的集合。 - 交集：A∩B表示同时属于A和B的元素集合。 - 补集：∁UA表示所有不属于A的元素组成的集合，U是全集。 4. 集合的运算性质： - 并集性质：空集与任何集合的并集等于该集合；集合与自身的并集仍是自身；并集交换律；A∪B=A当且仅当B⊆A。 - 交集性质：空集与任何集合的交集为空集；集合与自身的交集等于自身；交集交换律；A∩B=A当且仅当A⊆B。 - 补集性质：集合与其补集的交集为空集；集合与其补集的并集等于全集；补集的补集等于原集合；补集分配律。 5. 集合关系的常用结论： - 对于有限集A，其子集的总数为2^n，非空子集为2^n-1，真子集为2^n-1。 - 题目示例分析了集合关系的正确性和错误性，并提供了解答。 6. 应用问题： - 直线方程的交点形成一个集合，如直线y=x+3与y=-2x+6的交点构成的集合，可以通过解方程来确定。 - 已知集合A和B，根据交集和补集的运算可以求出特定条件下的子集，例如在给定的集合A和B中找到满足条件的B的子集。 集合论是数学的基础，掌握集合的概念、表示法、关系和运算性质对于解决各种数学问题至关重要。理解这些知识点，不仅对高中数学的学习大有裨益，也是进一步学习高等数学和其他科学领域所必需的。